全微分
解ける形の微分方程式として「全微分形である場合」があるので、その場合の解き方と、全微分形でない場合に全微分形に直していく方法について考えよう。ついでにこの後でも使う「偏微分」の記号に慣れておこう。
全微分形
そもそも微分方程式を解くとは、なんらかの意味で積分を行うことであった。微分を含むある式
\begin{equation} P({x},{y})\mathrm dx + Q({x},{y})\mathrm dy =0\label{kanzenkeikana} \end{equation}をなんらかの計算を行った結果として、
\begin{equation} \mathrm d \left( \fbox{なんとか}\right)=0 \end{equation}という形にまとめ直すことができれば、なんとか=定数と積分ができる。たとえば、
\begin{equation} ({x}^2+2{x}{y})\mathrm dx + ({x}^2-{y})\mathrm dy=0 \end{equation}という式は、
\begin{equation} \mathrm d \left({1\over 3}{x}^3 + {x}^2{y}-{1\over 2}{y}^2\right)=0 \end{equation}とまとめられる。
よって、
\begin{equation} {1\over 3}{x}^3 + {x}^2{y}-{1\over 2}{y}^2=C(一定) \end{equation}が解である。
(1) $2{x}\mathrm e^{{x}^2+{y}}\mathrm dx + \mathrm e^{{x}^2+{y}}\mathrm dy=0$
(2) ${{y}\over {x}}\mathrm dx + (\log{x})\mathrm dy=0$
(3) ${y}\sin{x} \mathrm dx -\cos{x}\mathrm dy=0$
このような手順も一つの微分方程式の解き方である。
この$\mathrm d \left( \fbox{なんとか} \right)$という形の式をなんとかの「全微分(exact differential)」(あるいは「完全微分」)と呼ぶ。そして、こういう形の式は「全微分形(exact)」(あるいは「完全微分形」)英語の形容詞は「exact」だが日本語では「微分」を補って使う場合が多い。になっていると言う。この定義から、全微分形ならその微分方程式が解けるのは言わば当たり前である。
${\mathrm dy\over \mathrm dx}=f({x},{y})$を例として考える。右辺の$f({x},{y})$は、${x}$と${y}$の両方を含む式である。微分方程式が「解ける」ということは、これから、(いくらかの計算の後に)\begin{equation} U({x},{y})=C(定数)\end{equation}という式(${x}$と${y}$の関係式)を導けたということである。逆に、この式を微分することで(あるいは、微分した後少々計算することで)上の式に戻るだろう。
これまでに解いてきた微分方程式の場合で、一定となる量$U({x},{y})$を列挙する(どうやって解いたかは思い出してもいいし、変数分離できる例なのでもう一度解くのも簡単なはず)。
| (1) | (2) | (3) | (4) | (5) |
| 微分方程式 | 変数分離した形 | 解 | 一定となる量$U$ | $U$の全微分 |
| ${\mathrm dy\over \mathrm dx}=-{{x}\over {y}}$ | ${x}\mathrm dx+{y}\mathrm dy=0$ | ${x}^2+{y}^2=R^2$ | ${x}^2+{y}^2$ | $2{x}\mathrm dx+2{y}\mathrm dy$ |
| ${\mathrm dy\over \mathrm dx}=-{{y}\over {x}}$ | ${1\over {x}}\mathrm dx+{1\over {y}}\mathrm dy =0$ | ${y}={C\over {x}}$ | ${{x}{y}}$ | $ {y}\mathrm dx+ {x}\mathrm dy$ |
| ${\mathrm dy\over \mathrm dx}={{y}\over {x}}$ | $- {1\over {x}}\mathrm dx+{1\over {y}}\mathrm dy =0$ | ${y}=C{x}$ | ${{y}\over {x}}$ | $-{{y}\over {x}^2}\mathrm dx+ {\mathrm dy\over {x}}$ |
| ${\mathrm dy\over \mathrm dx}={y}$ | $-\mathrm dx+{1\over {y}}\mathrm dy=0$ | ${y}=C\mathrm e^{{x}}$ | ${y}\mathrm e^{-{x}}$ | $ - {y}\mathrm e^{-{x}}\mathrm dx + \mathrm e^{-{x}}\mathrm dy$ |
というのが変数分離を使って解く微分方程式の解法だが、
という微分方程式の解法も有り得るこの場合、変数分離不可能でも解ける可能性が出てくる。。
この「全微分形に直す」という解法を考えるために、上の例それぞれの場合で(2)と(5)の違いを見てみよう。
${\mathrm dy\over \mathrm dx}=-{{x}\over {y}}$の場合 (2)と(5)は定数倍(2倍)違うが、同じ結果だと言える。
${\mathrm dy\over \mathrm dx}=-{{y}\over {x}}$の場合 (2)と(5)は${{x}{y}}$倍違う。
${\mathrm dy\over \mathrm dx}={{y}\over {x}}$の場合 (2)と(5)は${{y}\over {x}}$倍違う。
${\mathrm dy\over \mathrm dx}={y}$の場合 (2)と(5)は ${1\over {y}\mathrm e^{-{x}}}$倍違う。
以上の例から、解ける微分方程式であっても、単に$P\mathrm dx+Q\mathrm dy=0$の形にしただけでは全微分形にはなっていないこともあることがわかる。しかし、適当に何かの数もしくは関数を掛けてやることで全微分形に直していくことができる場合もある常にできるとは限らないが、これができるならこのやり方で解ける微分方程式だったということ。。
したがって微分方程式を「全微分形にする」という方針で解こうとするのであれば、方程式に適切な関数を掛けるという操作が必要になりそうである。
一つの可能性として、$U={x}^m {y}^n$という特別な場合を考えてみよう。$U$を微分すると、
\begin{equation} {x}^m{y}^n=C~~~を微分して~~~~ m{x}^{m-1}{y}^n\mathrm dx + n{x}^m{y}^{n-1}\mathrm dy =0\label{Uxy} \end{equation}となる。この逆に
\begin{equation} m{x}^{m-1}{y}^n\mathrm dx + n{x}^m{y}^{n-1}\mathrm dy =0 ~~~を積分して~~~~ {x}^m{y}^n=C \end{equation}であることを思いつければ微分方程式が解ける。すなわち、
\begin{equation} \underbrace{m{x}^{m-1}{y}^n}_{{x}^m{y}^nを{x}で\atop 微分したもの}\mathrm dx + \underbrace{n{x}^m{y}^{n-1}}_{{x}^m{y}^nを{y}で\atop 微分したもの}\mathrm dy =0\label{mxny} \end{equation}のように思いつけばよい。以上を頭に入れておくと、たとえば
\begin{equation} {y}\mathrm dx -{x}\mathrm dy=0\label{monenminusone} \end{equation}という微分方程式が出てきた時、「これは$m=1,n=-1$という状況では?」と予想することができるこういう予想が成立する為には、二つの項が${x},{y}$について同次(今の場合はどっちも2次)である必要がある。。二つの式を見比べるとこのままでは一致しないが、の両辺を${y}^2$で割ると、\begin{equation} {1\over {y}}\mathrm dx -{{x}\over {y}^2}\mathrm dy=0 \end{equation}となり、これが${{x}\over {y}}=(定数)$という式の全微分であることがわかる。微分方程式に出てくる項の${x},\mathrm dx$の次数と${y},\mathrm dy$の次数が一致しているような場合(ここで解いた式の場合、${x},\mathrm dx$の1次、${y},\mathrm dy$の1次だった)、適当な$m,n$見つけて全微分に直すことができる。
もっと一般的な形として、\begin{equation} f'({x}){y}\mathrm dx+f({x})\mathrm dy=0 \end{equation}のような微分方程式があったならば、\begin{equation} \mathrm d \left(f({x}){{y}}\right)=0 \end{equation}という形にまとめていくことで解いていくことができそうだ。
以下の微分方程式を適切な関数を両辺に掛けて全微分に直し、解け。
(1)~${y}\mathrm dx + 2{x}\mathrm dy=0$~~~(2)~$\mathrm dx+{1\over 2{y}}{x}\mathrm dy=0$~~~(3)~${y}\mathrm dx+\tan{{x}}\mathrm dy=0$~~~(4)~${{y}\over {x}}\mathrm dx+\log {x}\mathrm dy=0$
ここで、注意しなくてはいけないのは、$\underbrace{m{x}^{m-1}{y}^n}_{{x}^m{y}^nを{x}で\atop 微分したもの}$、すなわち
${x}^m{y}^n$を${x}$で微分して答は$m{x}^{m-1}{y}^n$になった
という時の「微分」は単なる微分とは違っていることである。というのは、この計算をやっている時、あたかも${y}$は定数であるかのごとく扱っている。実際のところ${x}$と${y}$は連動して変化する(たとえば$m=n=1$の例では${x}{y}$が一定だから、${x}$が増えれば${y}$は減る)のに、あえて変化しないと考えている。
このように、上の計算では、「実際は{変数}であるものを定数であるかのごとく扱って微分する」ということを行っている。
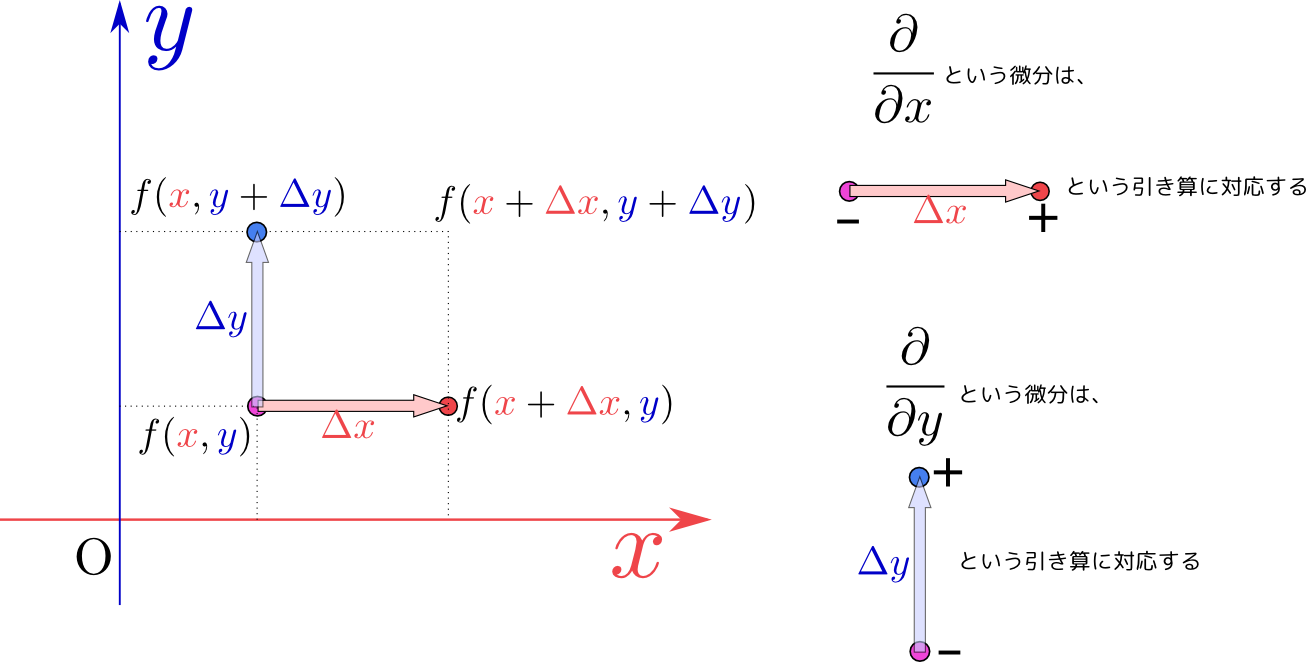
ここで、「変数を勝手に定数にしてはいけないのでは?」と悩む人が多いので注意しておこう。ここでやっていることは、${x}{y}$を一定にしつつ${x},{y}$を変化させているのだから、${x}$と${y}$は同時に連動して変化する。図示すれば次の図のような変化であり、同時に起きた二つの変化を「$y$の変化による部分(${x}\mathrm dy$)」と「$x$の変化による部分(${y}\mathrm dx$)」に分けて計算している。
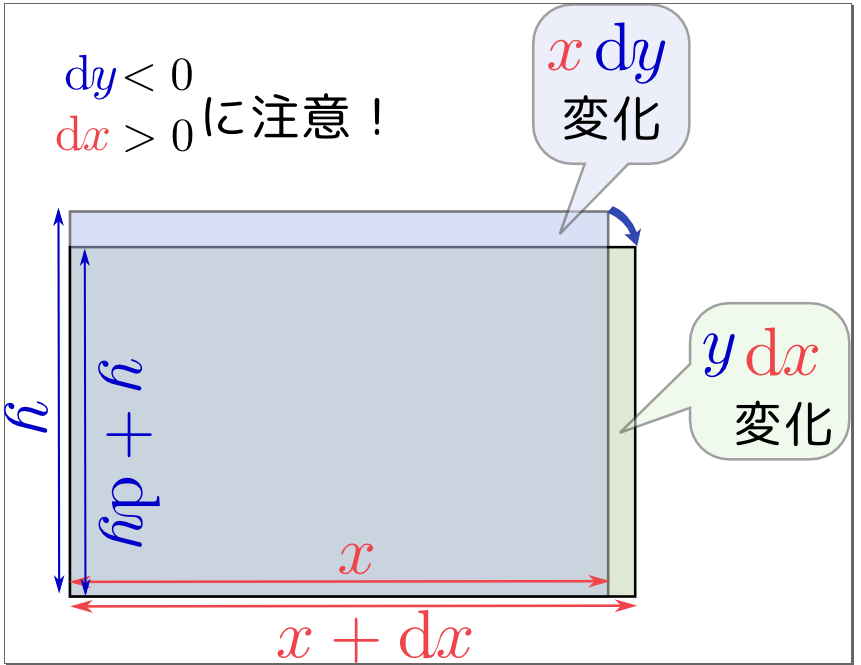
${y}$を定数にしたのではなく、${y}$の変化による部分は第2項で計算しているから、第1項では省いているだけのことである。変化するはずの${y}$は、ちゃんと変化させていて、その分は第2項で計算しているので、心配無用である。
次の節で、この新しい形式の微分に名前と定義を与えよう。