積分因子
まず全微分・偏微分の復習をしたのち、練習問題として
$y\mathrm dx+ x\mathrm dy=0$
という微分方程式を考えた。これは単純に
$\mathrm d(xy)=0$となって$xy=$一定が微分方程式の解である。
では、
$y\mathrm dx- x\mathrm dy=0$
はどうだろうか?
$\mathrm d(xy)$ではダメなのはわかる。この場合では全微分に直すことはできない。しかし、あきらめてしまう前に少し試行錯誤をしてみよう。
たとえば、$\mathrm d(x^2y)$を考えると、
$2xy\mathrm dx+ x^2\mathrm dy$
という式が出てくる。あるいは、$\mathrm d(xy^2)$を考えると、
$xy^2\mathrm dx+ 2xy\mathrm dy$
が出る。このように、指数が係数になって現れるということを考えると、$xy^{-1}={x\over y}$を使ってみればいいのでは?と思いつく。やってみると、
$\mathrm d(xy^{-1})=y^{-1}\mathrm dx- xy^{-2}\mathrm dy$となる。これは今解きたかった式の左辺$y\mathrm dx- x\mathrm dy$の$y^{-2}$倍である。
つまり、$y\mathrm dx- x\mathrm dy=0$はすぐに解けないが、これを${1\over y^2}$倍した、$\mathrm d(xy^{-1})=y^{-1}\mathrm dx- xy^{-2}\mathrm d=0$は、$\mathrm d\left({x\over y}\right)=0$となり、${x\over y}=$一定となって解ける!
このように解けなかった(積分可能条件を満たしてなかった)式に、何か式を掛けて解ける式(積分可能条件を満たす式)に変えよう、というのが今日の授業前半の目標である。
積分可能条件が満たされてなかったら全微分形ではない。しかし、ここで$P\mathrm dx+Q\mathrm dy=0$の右辺が0なので、両辺にある関数$\lambda({x},{y})$を掛けて
\begin{equation} \lambda({x},{y}) P({x},{y})\mathrm dx +\lambda({x},{y}) Q({x},{y})\mathrm dy=0 \end{equation}として、
を満たすことができれば全微分形ではなかった微分方程式を全微分形に直せたということになる。この掛算した$\lambda({x},{y})$のことを「積分因子(integrating factor)」と呼ぶ。積分因子は
\begin{equation} \begin{array}{rl}\left( {\partial\left( \lambda({x},{y}) Q({x},{y}) \right)\over \partial x}\right)_{\!\!{y}}-\left( {\partial\left( \lambda({x},{y}) P({x},{y}) \right)\over \partial y}\right)_{\!\!{x}}=&0\\ \left( {\partial\lambda({x},{y}) \over \partial x}\right)_{\!\!{y}} Q({x},{y}) -\left( {\partial\lambda({x},{y}) \over \partial y}\right)_{\!\!{x}} P({x},{y}) =& -\lambda({x},{y}) \left(\left( {\partial Q({x},{y})\over \partial x}\right)_{\!\!{y}}-\left( {\partial P({x},{y})\over \partial y}\right)_{\!\!{x}} \right) \\ \end{array}\label{lambdakettei} \end{equation} という方程式を満たせばよい。しかし、この式から$\lambda({x},{y})$の形を求めるのは一般には簡単ではない(また、この方程式の解$\lambda({x},{y})$は一意ではない)。たまたま、$\lambda$が${x}$のみの関数になるような場合はこの式が \begin{equation} {\mathrm d \lambda({x}) \over \mathrm d x} Q({x},{y}) = -\lambda({x},{y}) \left( {\partial Q({x},{y})\over \partial x}- {\partial P({x},{y})\over \partial y} \right)\label{lambdaketteij} \end{equation}という形になるので、少し解きやすくなる。
実際に解くときには、いろいろな場合を想定して試行錯誤を行う。
多変数関数とその微分
多変数関数
多変数関数と自由度
1変数の関数とは、「独立変数と呼ばれるある量$A$を決めると、従属変数と呼ばれる、それとは別のある量$B$が決まる」という対応関係であった。
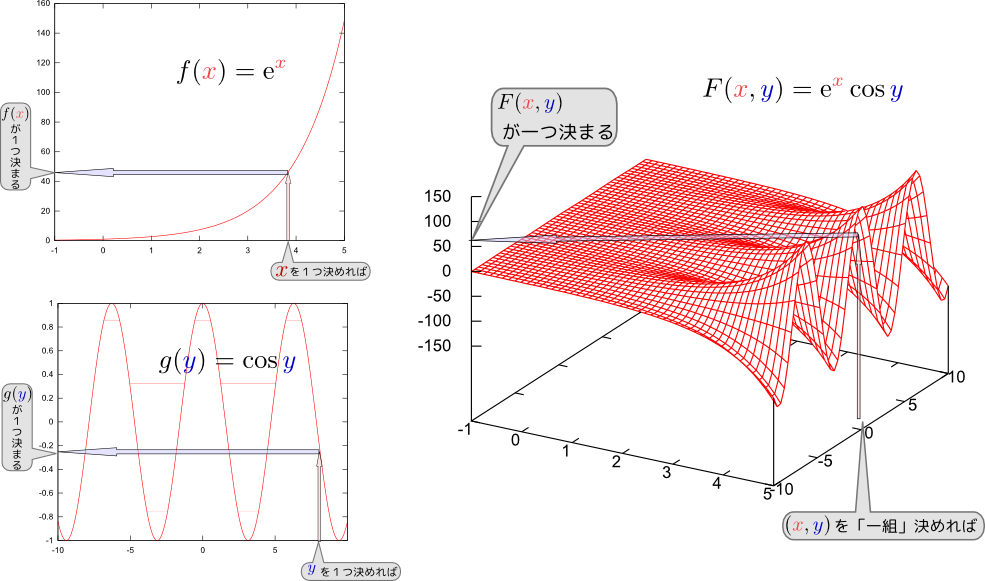
独立変数が一つの量ではなくなり、「独立変数ある一組の量$A_1,A_2,\cdots$を決めると、従属変数ある量$B$が決まる」という対応関係(もちろん、「ある量」はただひとつに定まらなくてはいけない)となったものを「多変数関数」と呼ぶ(この「多」は「独立変数が複数」という意味である)。たとえば、${x},{y}$を決めると${z}$が決まる、という対応関係(この場合は「2変数関数」である)なら、${z}=f({x},{y})$のように書く。例をあげておくと、$f({x},{y})={x}{y},f({x},{y})={x}+{y},f({x},{y})=\mathrm e^{{x}}\cos {y},\cdots$など、いろいろな場合がある。少し意味のある例を上げると、${x}$-${y}$平面上で原点と$({x},{y})$の間の距離は$f({x},{y})=\sqrt{{x}^2+{y}^2}$という式で表される2変数の関数は「平面上の点を一つ決めるとある値が決まる」という関係であることが多いが、これに限るわけではない。たとえば空気の密度$\rho$は温度$T$と圧力$p$で決まるから、$\rho(T,p)$のような2変数関数で書ける。。
1変数の関数は、独立変数と従属変数という二つの変数を持っているが、独立変数一つを決めれば従属変数も決まったから「自由に動かせる数」は一つであった。これを「自由度1」と表現する。2変数の関数の場合、二つの独立変数を決めると従属変数が決まるから、「自由度2」である(三変数、四変数と増えていっても同じである)。
1変数の関数は${x}$-${y}$という平面の上に描かれた「線(一般には曲線)」で表現された。線は「自由度1」あるいは「1次元」の存在である(つまり、線の上の点は1方向にのみ動ける)。同様に2変数の関数は「面(一般には曲面)」で表現されることになるそもそも「次元」というのは「自由に動ける方向の数」を意味する(1次元なら線、2次元なら面、3次元なら立体)。。
次に、$f({x},{y})=\mathrm e^{{x}}\cos{y}$という2変数関数の「立体グラフ」を示そう。
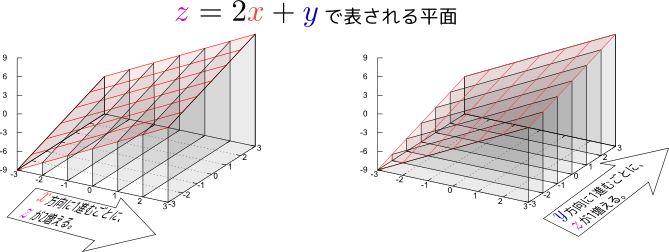
非常に単純な2変数関数${z}=f({x},{y})=a{x}+b{y}+c$を考えると、これは$({x},{y},{z})$という3次元空間の中にある(傾いた)平面を表現している。原点$({x},{y})=(0,0)$に置いては${z}=c$で、${x}$方向に移動すると移動量$\times a$だけ${z}$が増え、${y}$方向に移動すると移動量$\times b$だけ${z}$が増える。増加量が移動量$\times$(一定値)となる場合、この図形は平面になる。
多変数の微分
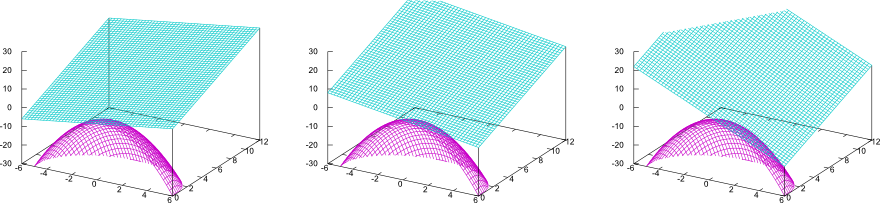
1変数のときの微分または微係数とは、「関数のグラフを拡大していけば直線のグラフになる(これは微分可能な関数に限る)から、その直線の傾きを求める」というのがその定義であった。2変数の場合の「グラフ」は線ではなく面になるが、この面も(微分可能な関数なら)拡大していけば平面になり、その平面の傾きに対応するものが偏微分なのである。

上の図は簡単な2変数関数$f({x},{y})=-2{x}^2+{x}-2{y}^2+2{y}$の図と、それに接する平面(接平面)の図である。接平面の接点が原点$({x},{y})=(0,0)$であるとき、接平面は$f({x},{y})$から${x},{y}$の2次の項を省略した${x}+2{y}$である(原点付近では2次の項は小さいので無視できる、という考え方をする)。また、$({x},{y})=(1,0)$における接平面は、まず$f({x},{y})$を
\begin{equation} f({x},{y})=-({x}-1)^2 -({x}-1)-2{y}^2+{2}{y} \end{equation}と書きなおしてから$({x}-1)$に関して2次の項を消せばよい(こうして${z}=-{x}+1+2{y}$を得る)---のだが、そんなことをしなくても偏微分の結果${\partial f({x},{y})\over \partial x}=-2{x}+1,{\partial f({x},{y})\over \partial y}=-4{y}+2$に${x}=1,{y}=0$を代入すれば係数($-1$と$2$)は計算できる。図に描き込んだ$(2,0)$の場合も同様である(確認してみよう)。
次の図は、上の接平面の図を、接点の部分にあたる、${y}=0$で切断した様子である(切断面が二次関数$-{x}^2+{x}$となり、接平面が接線になっていることがわかる)。