青字は受講者からの声、赤字は前野よりの返答です。
先週やっていた事をけっこう忘れていたので、授業が週一回しかないのはおそろしいです。復習がんばります。
授業で勉強終わりじゃなくて、プリントをまとめて読み返したり、あるいは授業ホームページに行ってプログラム動かすとかやってみてください。
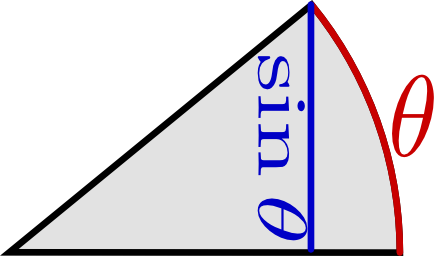
どうしてラジアンで角度を表すと便利なのかわかった。sinθとθの関係が面白かった。
sinθとθが角度が小さいと同じになるのも、ラジアンで表しているおかげですね。
三角関数で、ラジアンの単位に直す意味とか考えたりした事なかったので、考えて学べて楽しかったです!! sinθの計算もおもしろかったです。
計算するからには、何かしら意味はあります。そこを理解していきましょう。
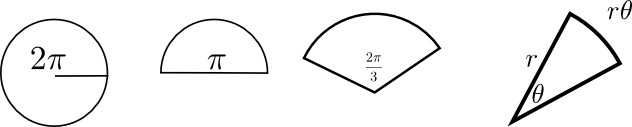
ラジアンが、円周の長さ2πrを基準にしているのはびっくりした。
$\sin^2\theta+\cos^2\theta=1$の式はとてもよく理解できた。
どんな式や決まりにも由来というのはあるので、そこを知って理解していきましょう。
一周が360度の理由が割り算行いやすいというもので驚きました。もっとすごい理由があると思ってました。
割り算が簡単(約数が多い)ってのはすごく大事なことですよ。
ラジアンのところは今までなんとなく使っていましたが、今回は納得できてよかったです。
「なんとなく」は駄目ですよ、何事も。
ラジアンが2πの理由がわかった。
理由わからないで使っていると気持ちわるいですよね。
ただ公式を覚えるよりも図やグラフを書いて理解した方が記憶に残るし楽しいと思った。
どんな式にも意味はあるので、そこをじっくり理解しましょう。
三角関数は難しい。苦手なので、しっかり理解して進みたい。
苦手意識は早めに克服しましょう。
sinθ、cosθ、tanθの意味が詳しく分かった。でもやっぱり苦手。
意味を考えたうえで、得意にしていってください。
三角関数の復習をして、思い出した、公式を。
図で理解して、忘れないようにしましょう。
$\sin\left(\theta+{\pi\over2}\right)=-\cos\theta,\cos\left(\theta+{\pi\over2}\right)=\sin\theta$って$\cos\left({\pi\over2}-\theta\right)=\sin\theta,\sin\left({\pi\over2}-\theta\right)=\cos\theta$より大事ですか。
使う場面が違うので、どっちも大事。
高校の復習だったので、これからの大学の勉強のために、おこたらず、やっていきたい。
少しずつ大学の数学が染みこんできてますよ。
今まで数学は得意だと思っていたけど、実際の意味を知らなかった事に気付かされた。真の数学の力をこの授業で身につけたい。
数学は(そして他の自然科学も)とても深いです。掘れば掘るほど意味が湧き出てくる。
公式も今まではただ覚えているだけだったけど図で見るとどうしてそうなるのかがすぐ理解できて、楽しかった。
「ただ公式覚えるだけ」なんていうつまらない勉強はしちゃ駄目ですよ。
三角関数は昔から苦手で、イメージもしずらかったので、タブレットや説明などを聞いて理解できたのでよかったです。
今度こそ苦手を克服してください。
sin,cosを図で見るとまた違った感覚で見れるので想像しやすくて面白かった。
三角関数は幾何学からくる関数なので、図で理解するのが一番です。
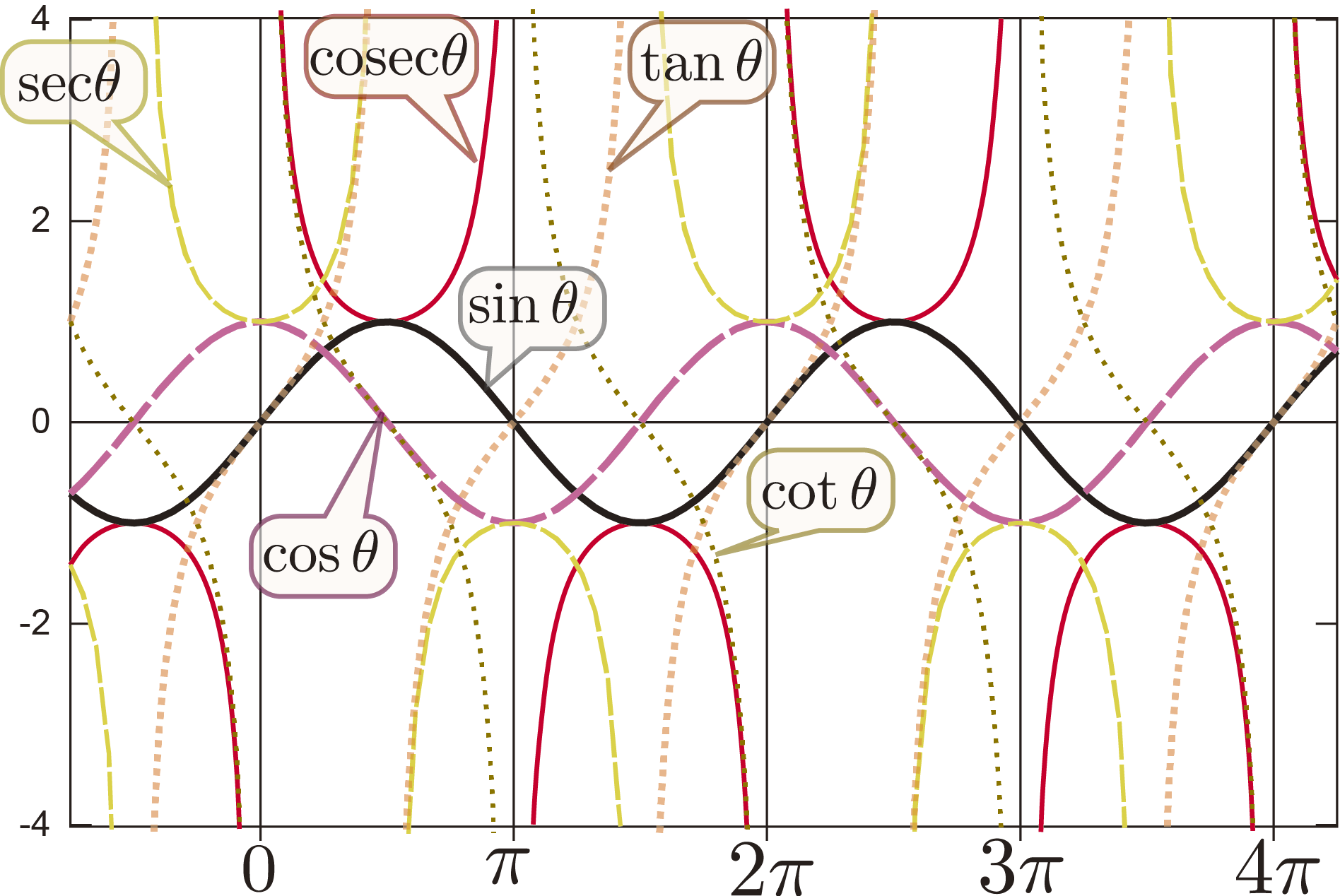
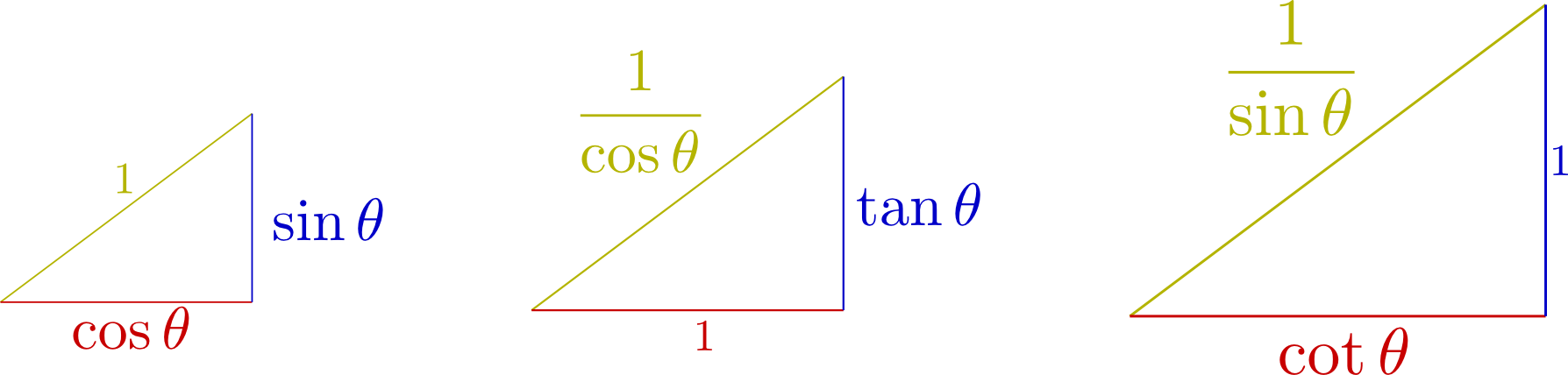
三平方の定理から三角比を出したことはなかった。sin,cos,tanの逆数にも名前があることを知った。これからよくお目にかかることになるのかな?
「よく」ではないですが「たまには」出てきます。
cotθやcosecθがあるのは始めて知った。$\sin^2\theta+\cos^2\theta=1$などの式を暗記していたので三平方でやった方が簡単だと思った。後先生の曲線がきれいだと思った。
図でわかることは図で理解した方がいいですよ。曲線ってなんだろう??
三角関数の公式を図や式で理解した。やっぱ公式は覚えるのではなく理解すべきものだと改めて思いました。
もちろん、その通りです。覚えるだけではつまらない。
cos,sec,cot。始めて聞きました。
タブレットって指が乾燥していたら反応しなかったりしますか?
乾燥していると反応しにくくなることはあります。
三角関数についてよくわかりました。特に三平方の定理で三角関数の関係式を出せることは始めて知って納得できました。
う〜ん、意外と知らない人いたりするんだなぁ。
sin,cosの変動ぐあいみたいなのを改めて実感しました。
実感を持って関数を使いましょう。。
三角関数の根本的な性質、また高校で習った相互関係の式を図で理解しました。相変わらず今日も楽しい授業で、今まで習った分野での新しい発見がたくさんあった授業でした。
楽しく勉強できているようで、何よりです。
始めて聞いたcosecθやsecθなど、まだまだ数学でわからないことがあるとわかった。
まぁcosecやsecは単に逆数ですから「わからないこと」と言っても可愛いもんです。
$\sin^2\theta+\cos^2\theta=1$などの暗記で覚えてた式の成り立ちがわかってよかった。
グラフや図から理解していきたいと思った。
こういう幾何学的な式は図形で理解しないと。
三角関数という分野は30度を${\pi\over6}$と表記したりするπの導入があって、僕は度で考えるので(みんなそうだけど)πに直したりする時に計算ミスをよくしました。
最初からラジアンで考えればよいんですよ。自然科学をやる人にとっては「ラジアン」の方が普通で、「度」はむしろ使いにくい。
「三平方の定理から公式を導く」というのが目からウロコでした。
う〜ん、高校の数学の教科書にも載っているはずの話なんだけど。
図で理解するのがとても苦手です…。この授業で慣れるといいな。(´ω`)今日いいことがあるとうれしいです。すずしい。てんてんてん。
自分が理解しやすい方向から理解して、その上で他の考え方にも慣れていく、というのがいい方法です。式が得意ならそっちを手がかりにして考えたっていいんですよ。ま、いいことはそのうちあります。
三角関数は難しいイメージだったけど、今日の授業を聞いて、できそうだと思った。
得意になってくださいね。
三角関数の公式はよく忘れますが、これからは憶えなくてよさそうです。
「憶える」じゃなく「理解する」ことが大事。
タブレットを使うことでsinθやcosθの動きがよくわかった。
イメージで理解しておきましょう。
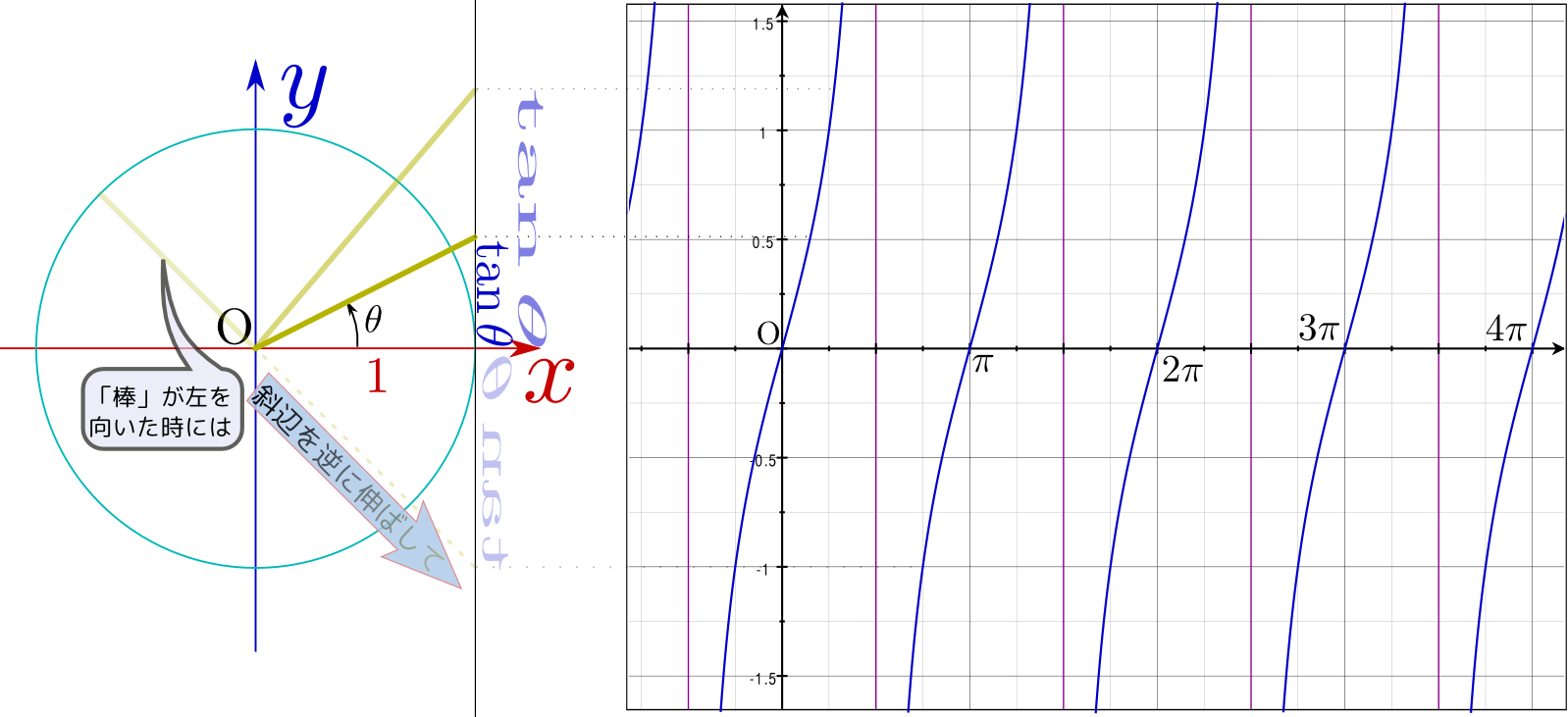
tanθのグラフはドラクエのワールドマップのように見えますね。
う〜ん、ドラクエのマップがわからないからコメントできない。
憶えにくかった公式が図で簡単に理解ができると知って感動した。
ほんとはあの公式は図から出てくるものなんですが。
sin0.1,sin0.01とかあたりまえのことだけどあ〜!!となった。図をぐるぐるするの楽しかった。
電卓一個でもけっこう遊べるもんなんですよ。
三角関数は図で理解すること!! 納得しました。今一度、図を書き、理解してきます。
図をたくさん自分で書くと、また理解が進むと思います。
今日は三角関数を学んだ。公式はああやって図形といっしょに憶えると理解が深まるのでそうしようと思った。
特に三角関数はもともと図形のための関数なので、図は大事。
高校で習った三角関数の公式がよくわかった。
図を書いて理解していきましょう。
三角関数の式の作り方を今まで知らなかったので今日知れてとてもよかった。これから三角関数をもっと深く学びたい。
式の由来ってのは大事です。
sinθやcosθやtanθの逆数がcosecθやsecθやcotθというのを始めてしりました。
これから先、また出てくるかもしれません。
図だとすごくわかりやすかったです。θを180度以上にした時の図がすごかったです。sin0.1,sin0.01などの計算のしかたが気になります。
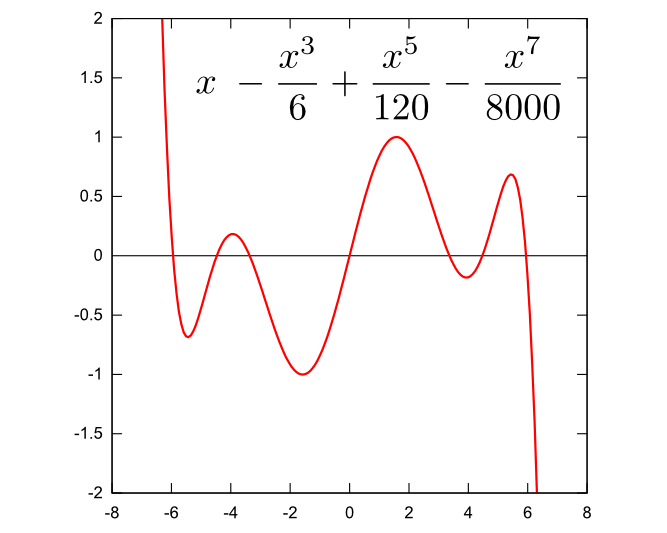
sin0.1をどうやって計算するのかは、この後のお楽しみに。
sin0.1,sin0.01,sin0.001が、十の位ずつずれて小さくなっているのにびっくりし、さらに角度を小さくすればsinθ≒θで、0.09983‥はsinθとθの差になっていて、すっごく面白い、と思いました。
しばらくすると、どういう式でこういう計算になるか、を授業で説明しますね。
なんとなく使っていただけの三角比のことがようやくわかった気がしました。
「なんとなく使う」のはつまらないので、しっかり理解して、使いこなしましょう。
三角関数の定義を再確認することで、より理解が深まった。
定義を把握したうえで、理解していきましょう。
今回は三角関数について学んだ。cosec,sec,cotを始めてみたので、大学の数学らしいことをしていると実感した。また図を使うと三角関数の関係式を簡単に考えられることがわかった。
大学の数学っぽい数学は、これからもどんどんと出てくるでしょう。
高校で勉強した三角関数の復習もできた。物理でも三角関数を使うのでしっかり使えるように勉強していきたい。
三角関数はこれからもお世話になります。
三角関数のイメージがわきやすくてわかりやすい。
イメージをしっかりつかんでおこう。
タブレットで三角関数のグラフや図をいじるのが三角関数の特徴をとらえやすくて、分かりやすかった。授業を欠席すると損するなと思った。
そりゃ、損です。
当てられて答えられなかったのがくやしかったです。でも、おかげで先週の授業もわかってないと知ることができたので、しっかり復習しようと思いました。
次はいけるように。復習がんばりましょう。
図が動いての授業は楽である。sin,cos,tanの動きが苦手だったがおもしろかった。
動きでイメージつかんでください。
三角関数のグラフがタブレットで視覚的にわかりやすく理解できました!
どんな関数か、覚えておいてください。
表示などがおかしくなるときはページをリロードしてください。

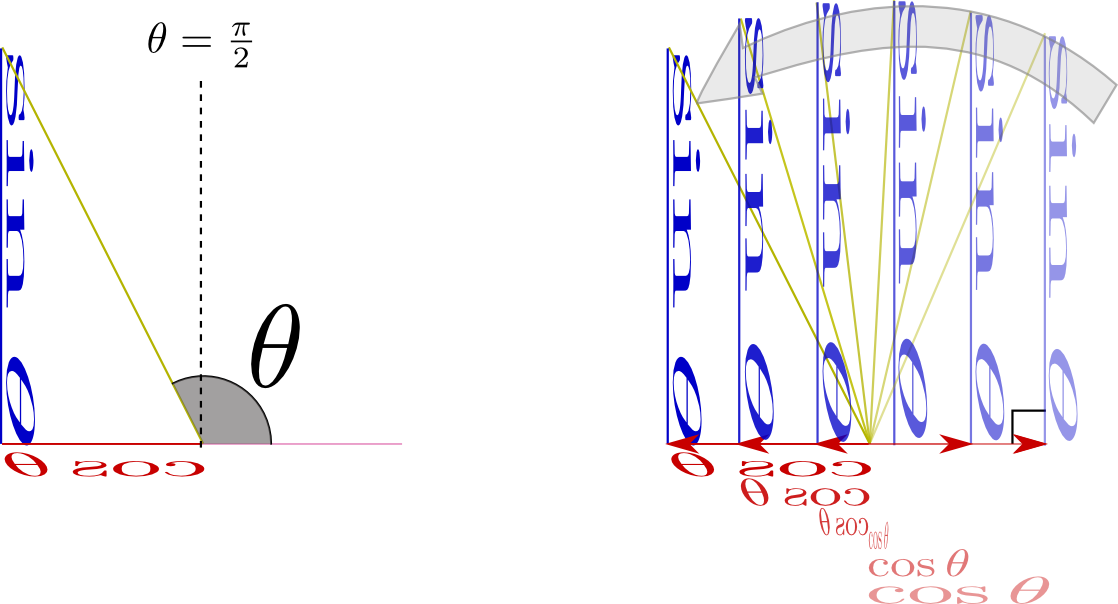

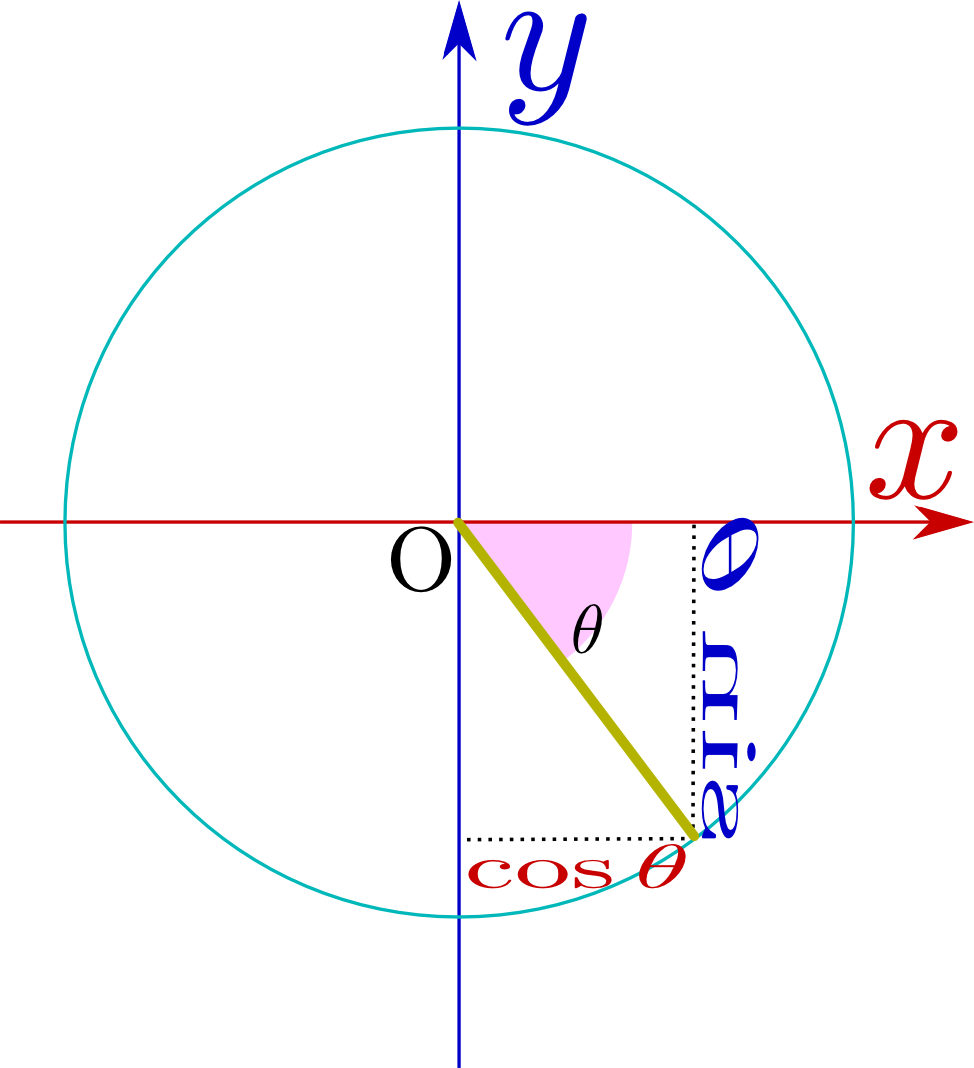
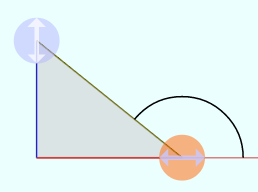 のようにθが直角より大きくなり「
のようにθが直角より大きくなり「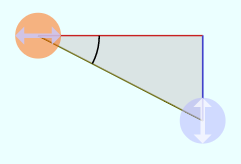 のようにθが負になり「
のようにθが負になり「 から
から に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを
に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを や
や が鏡文字になることで表現している。
が鏡文字になることで表現している。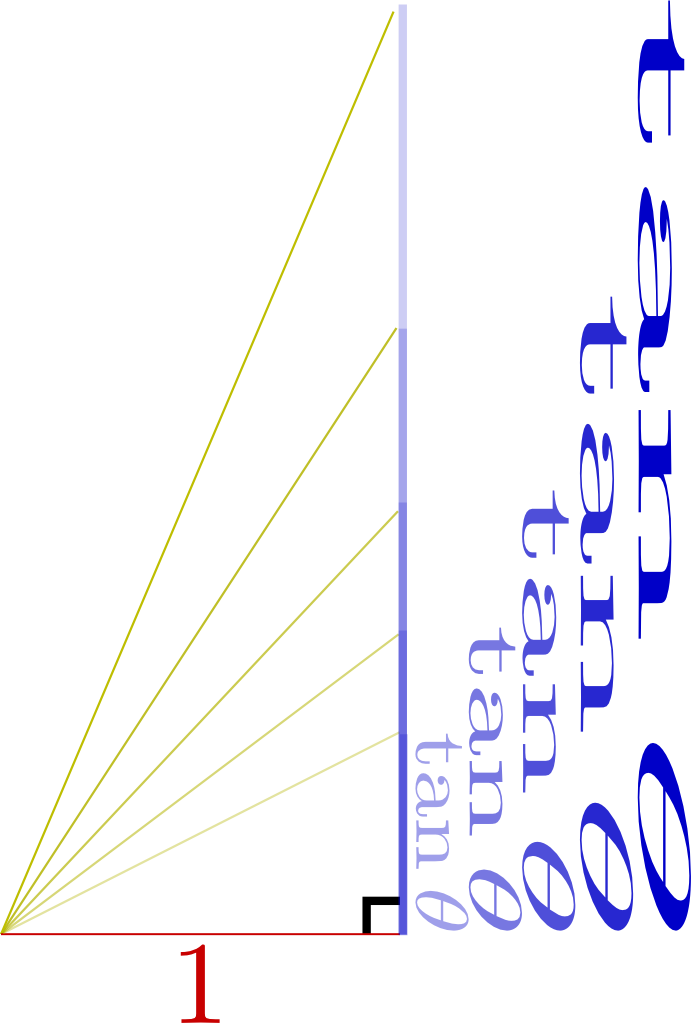
 は半径1の円(単位円)を描いたもので、中心から円周の一点に向かっている棒
は半径1の円(単位円)を描いたもので、中心から円周の一点に向かっている棒 の角度に応じて、
の角度に応じて、 のように2πより大きい(何周も回る)角度にしたり、
のように2πより大きい(何周も回る)角度にしたり、 のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。
のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。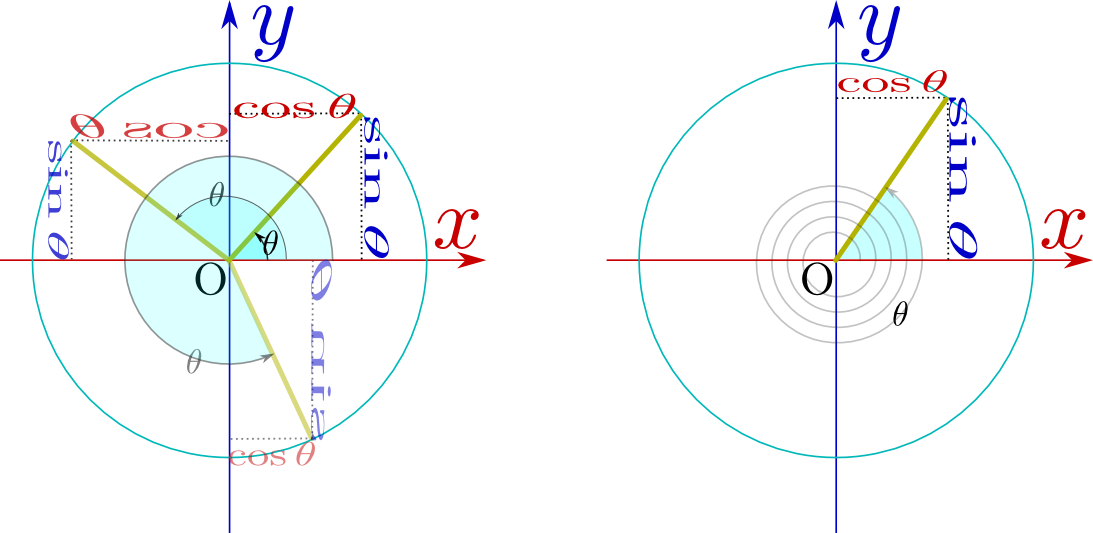
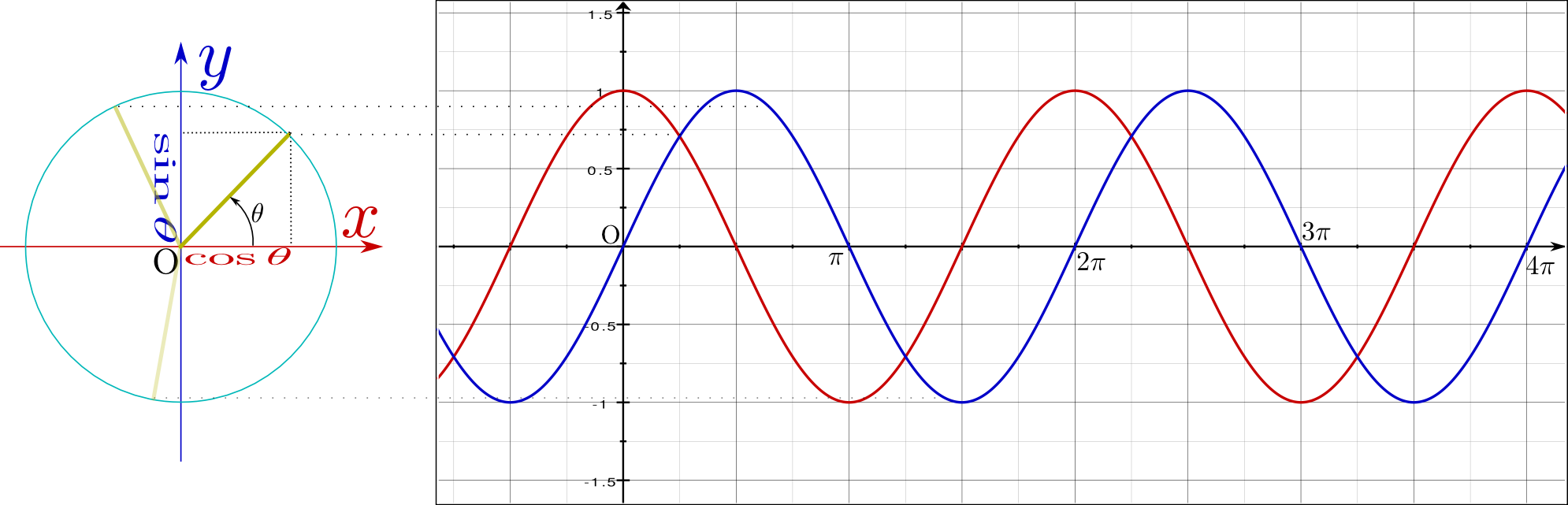
 の部分の薄い色になっている
の部分の薄い色になっている の方が、θよりπラジアン(180度)大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる(この公式は式として覚えようとしなくても、意味を考えればすぐにわかる)。
の方が、θよりπラジアン(180度)大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる(この公式は式として覚えようとしなくても、意味を考えればすぐにわかる)。