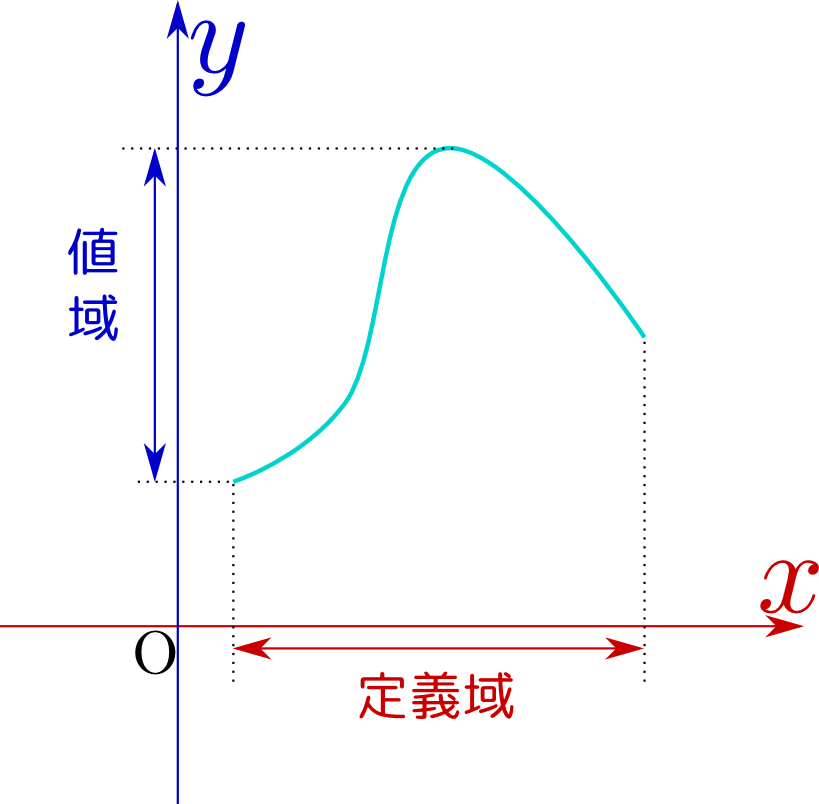
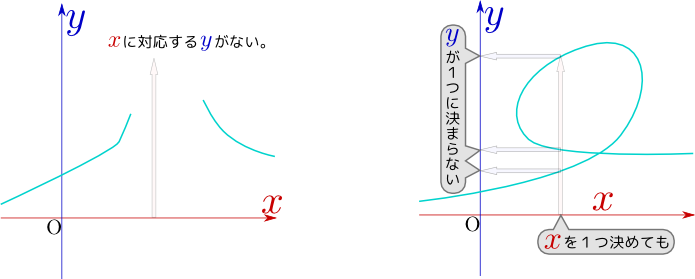
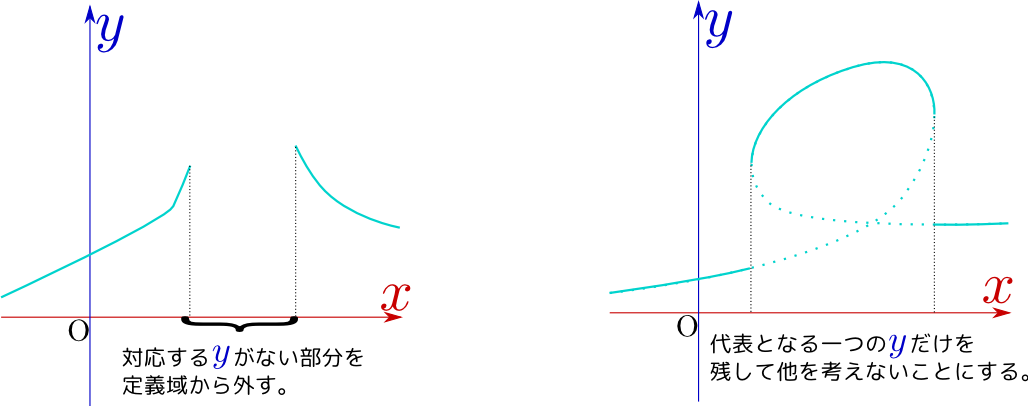
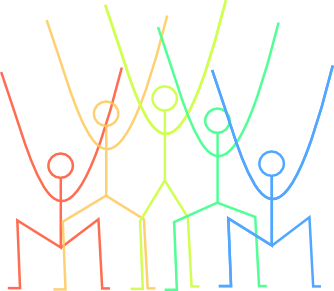青字は受講者からの声、赤字は前野よりの返答です。
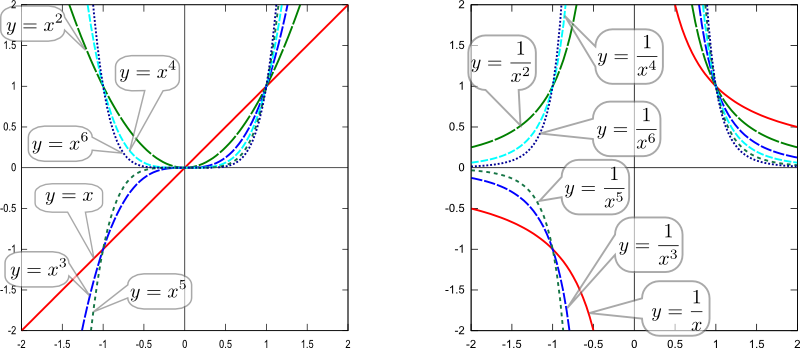
0〜1付近の次数式の差がつく所を知ることになった。
それぞれの関数の性質を身につけていこう。
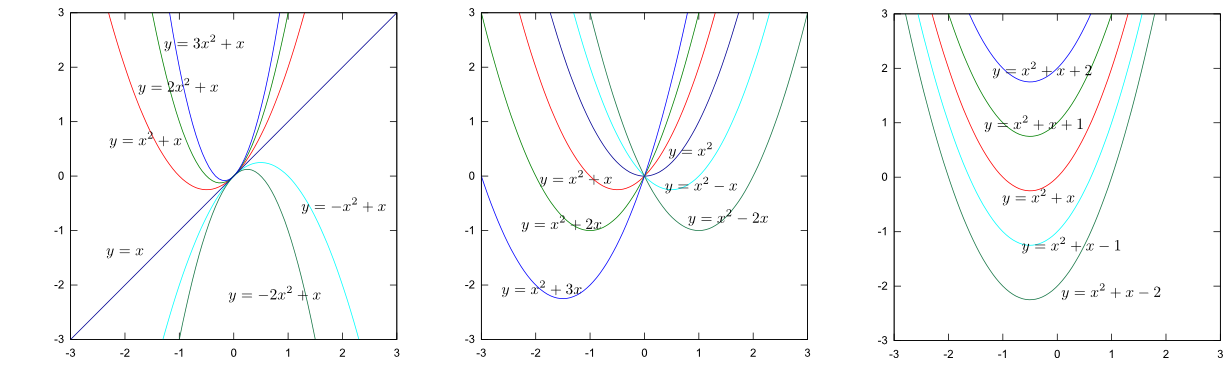
関数が□x3+□x2+□x+□のように□をいじって変化を追うのは面白かった。高校でもやって欲しかった。
これから先は高校でもどんどんやるようになるかもね。
関数のどのパラメータを変化させるとグラフでどの部分が変化するのかイメージしやすくなった。xnの変化でグラフがどのように変化するのかもわかった。
その変化のイメージを大切にしていこう。
先生が手足を動かしながらグラフを表現していたのが面白かった。関数の意味をちゃんと理解できてよかった。
「面白かった」で終わらずに、イメージを掴んで身につけてね。
関数の意味と、x3,x2,xの各々の役割がわかった。先生の動きで分かりやすかったです。
自分でもやってみて、身体に覚えさせよう。
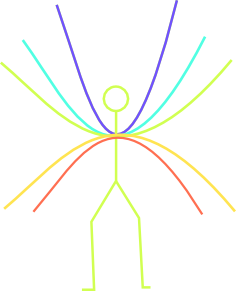
曲線が変数によってどんな変化をするのかがわかった。
それはよかった。
タブレットを使って関数の形や性質を眼でみることによって数式から図をイメージすることができました。イメージすることは大切だと思いました。
イメージをどんどん作っていきましょう。
今日も高校で習っていた関数の分析?意味的なことを考えてなるほど!と思える授業だった。他のものも自分でみつけてみたい!
やってみよう。自力でやるのが一番。
計算上だけで関数をグラフを見ながら関数の形を深く考えるのは初めてで、新鮮だった。
深く考えましょう。数学は深く考えるほど、面白い。
グラフからいろんなこととつながってておもしろかったです。ちなみにn=1782までいきました。
だ〜か〜ら〜。nをそんなに増やしたってもうそんなにグラフは変わらないでしょうに。
3次式2次式の係数によってグラフの変化する位置や形が変わっているとわかった。
式が出てきたら「このパラメータの意味は?」とかいろいろ考えていこう。
多項式のパラメータの意味がやっとわかった。
それはよかった。
関数のパラメータについて3次関数については初めてやったので楽しかった。
他の関数についてもいろいろ考えてみてください。
今日はグラフの性質を学びました。2次関数や3次関数のグラフの性質をみつけることができました。今日も楽しい授業でした。
楽しく、数学しましょう。
前から関数の定義は知っていたが、今回初めてアニメーションで振り返ることができた。自分で関数を作るソフトはかなり興味をもった。
いろいろ試してみましょう。パソコンや携帯などで手軽にグラフ書いて動かすソフトとしては、
geogebraなんてのもあります。
関数の文字の係数の意味ついて深く理解できた。少し前より数学に興味がもてた。
数学も興味を持ってやっていけば深く深く理解できるはず。
いろんなグラフがあって楽しかった。がんばります。
楽しく、がんばりましょう。
先生のシャツのボタンがはずれていたが、いつのまにかとまっていた。タブレットでの授業はやはりわかりやすい。
はて?(←シャツのボタンのことなんて気にしてない)。
y=ax3+bx2+cxのa,b,cに対応する動きを探すのは楽しかった。
しっかり理解しておきましょう。
いろいろな関数のグラフを係数を変えてみたりして決まり事を見つけるのが、とても楽しかったです。少し変えるだけでグラフが変わっていくのが実際見れてよかったです。
試してみて、頭の中にイメージを作っていきましょう。
関数の独立によって従属が決まることがわかった。
多項式の関数の一つ一つのxの役割がよくわかったので、グラフを書くときイメージができるようになるはず!
グラフと式と、そしてそれの表す自然現象とをイメージできるようになりましょう。
タブレットを初めてつかったのですが、なかなか反応しなかった。
3次関数の性質などほとんど忘れていた。
あれ、おかしいな?そういう時は声かけてください。
忘れてしまうような勉強はしないように。
グラフも式も項を1つずつみていくとそれぞれに傾きや形という意味があってとてもおもしろいと思った。
どんな式のどんな部分にも「意味」があるはずです。
図をみることでそれぞれの項の意味を理解することができた。
意味を理解してこそ、数式を使うことの利点が見えてくる。
グラフを使うと関数の特徴が見てわかるので考えやすかった。グラフを作った人はすごいと思う。
そういえば最初にグラフってものを作ったのは誰でしょうね。
式の値の一つ一つが変化するたびにグラフの値が変わるというのを改めて実感した。
実感とイメージを大切に。
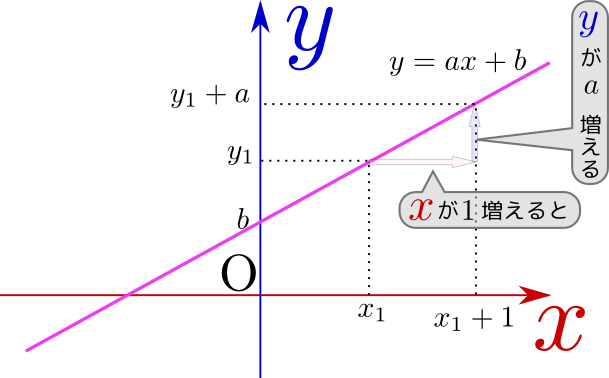
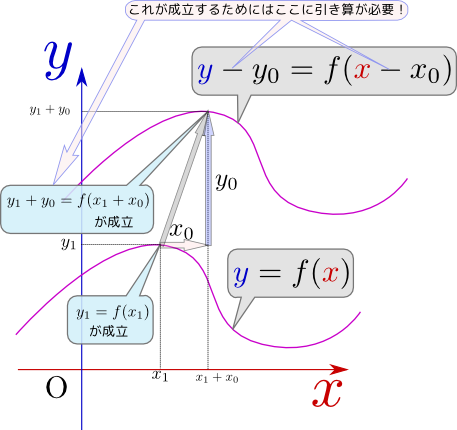
b,cの変化ではグラフの形は変わらずにグラフの平行移動だということがわかった。
平行移動とはどういう計算か、もしっかり理解しておこう。
関数のグラフについて新しい発見があり感動した。高校で学んできた数学より深く学べて楽しかった。
グラフというのは、こういうふうに関数をイメージしていくためのものです。
今日は、わかっていても恥ずかしくて答えられませんでした。高校ではとても嫌いだったけど、最近少しずつ分かるようになってきて、とても楽しいです。
わかってたら恥ずかしがることないのに。とにかく、楽しんでいきましょう。
今日は、グラフの性質がわかり高校までの内容がより理解が深まったと思う。
そして大学数学へと理解を進めましょう。
グラフの式の係数に一つ一つやくわりがあるのが面白かった。
もちろん、どんな式のどの部分にも何かしらの役割があります。
実際にグラフを見ることで関数とはなんぞやということがよく分かり、関数に注目することで今までわからなかったことがわかった。
いろんな方向から関数を理解していきましょう。
とてもわかりやすかった。もっとイメージできるようにしたい。
いろんなイメージをつけていこう。
今日の授業でもっとグラフが書きやすくなりました。数学でいつも図に書いて解いているのでとても為になりました。
図を書いて考えるのは大事です。
今日は多項式関数の1次や、2次の性質を学んだ。
よく理解しておきましょう。
数学が数字や数式だけではなく「自然科学のため」というのをより実感できました。
もちろん、その通り。
関数に関して別の見方(視点)を持てたように感じました。これからどんな関数を見るときにも傾き、曲がり具合を意識したいと思いました。
いろんな視点から、関数を見てみてください。
x3やx2を無視してみることでxがどんな役割をしているかわかった。
頭と心にそのイメージを刻みつけておきましょう。
色々なグラフを自分が変形してみると面白いしわかりやすいので、中高の時から導入すべきだと思います。
いずれ導入されていくと思いますよ。
(これは、前回「タイムマシンの話してたのは前野先生ですか?」と聞いた人)やはり、そうでしたか。あのお話のおかげで、私は物理学者を志しました、というとすおになります。
うそなんか〜〜〜い!
y=ax2+bx+c→パラメータの意味が理解できました。タブレットにより、実感できました。
動く図でイメージをつかんでおいてください。
多項式の次数に着目して、グラフの視認的な性質を把握した。
把握したことを身につけていこう。
係数変えたときの変化がタブレットで何回もみれるからすごくわかりやすかったし先生のジェスチャーで理解が深まりました。
繰り返しは大事ですね。
いろんな関数のグラフをタブレットのおかげでイメージできた。グラフの違いを言葉にするのが意外と難しかった。
数式、グラフ、そして日本語。どれでも「数学」を表現できる。できるようになろう!
パラメータの話を始めて聞いて、傾きや尖り具合がとても大事なことだと分かった。
後で出てくる「微分」の考え方です。
高校のときも身をギセイ(?)にして関数の形や移動を教えてくれた先生がいてなつかしく感じました!。余談ですが今朝起きたら喉がとても痛くて風邪を引いたのだと思います。前野先生もお気をつけてください(>_<)。
そちらこそお大事に。
グラフや関数の式のどこに注目するポイントがあるか少しわかった。
いろんな関数、それに応じていろんなグラフがあります。注意してみてください。
琉球大学理学部在籍の学生には関数の変数も「東・南・西・北」にする人がいて、マージャン好きの間ではやりました。先生も日本人の心の数学を是非はやらせてください。
マージャンはどうかと思うけど、東西南北は使いたい文字だねぇ。
なぜこのグラフになるかを考えるととても楽しい。頑張る。
いろんな関数において、そういう楽しみを見つけてください。
係数によってそれぞれグラフの形や位置などを帰るのをタブレットでやるとわかりやすかった。パラメータの働きはそれぞれ決まっていることがわかった。
理解を身につけていきましょう。
高校と違ってxやyなどの文字が決まってないことがわかった。
いや、高校の範囲でも違う文字を使うことはありますよ。
グラフの平行移動は今まで特に理由など考えたことがなかったのでとても興味深かったです。
「なぜこうなる?」という理由を考えていかないと、活きた自然科学にならないので、そこは興味を持っていきましょう。
表示などがおかしくなるときはページをリロードしてください。
 →「多項式関数」をダウンロード(←クリックでダウンロードできない場合は「リンク先を保存」をしてください)
→「多項式関数」をダウンロード(←クリックでダウンロードできない場合は「リンク先を保存」をしてください)
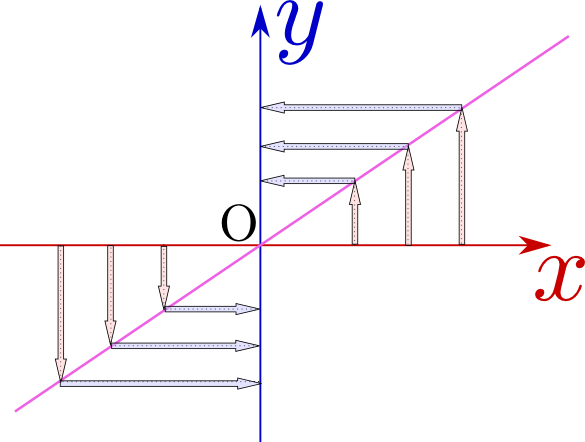
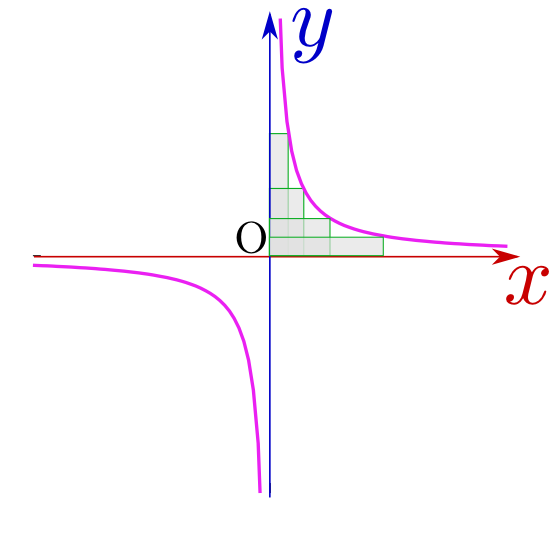
 を動してxを変化させると、それに応じて
を動してxを変化させると、それに応じて つまりyが動く。yの方は動かせません。「従属」変数ですから。
つまりyが動く。yの方は動かせません。「従属」変数ですから。