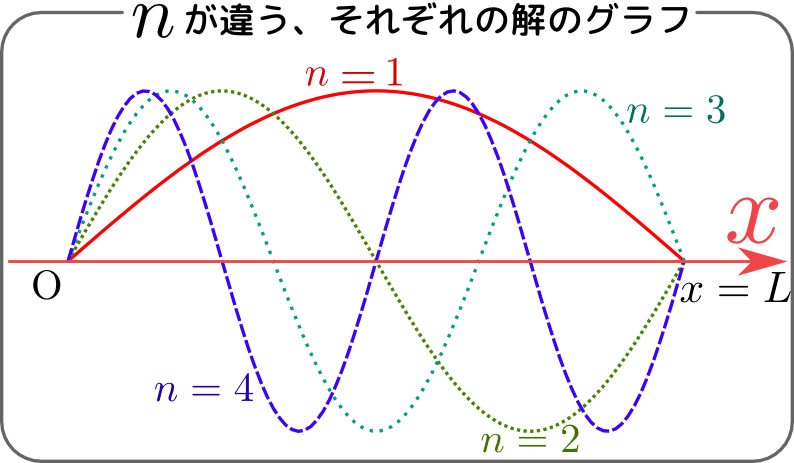
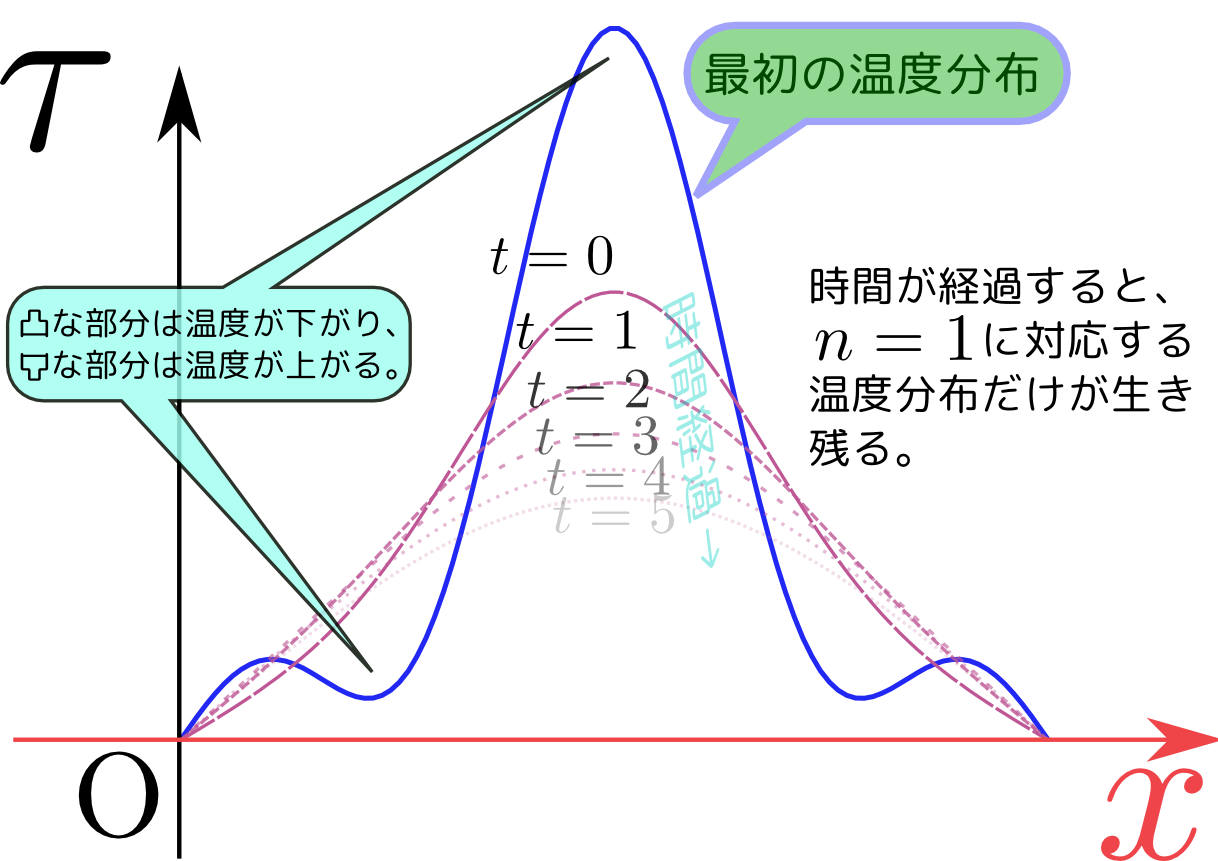
偏微分方程式の解き方
ここまで考えた微分方程式は常微分$\left({\mathrm d\over\mathrm dx},{\mathrm d\over\mathrm dt},\cdots\right)$を用いた微分方程式だったが、偏微分$\left({\partial\over \partial x},{\partial\over \partial t},\cdots\right)$を用いた微分方程式もある。
簡単にその解き方を紹介した後、いくつかの実例を示そう。
以下では、求めるべき関数を$f({x},{y})$のように二つの独立な変数${x},{y}$によって決まる2変数関数として説明する。変数が${t}$になったり${r}$になったりしても考え方は変わらないし、3変数、4変数と変数の数が増えても、基本的には同様の手順で解いていくことになる。
変数分離による解法
\begin{equation} \left({\partial\over \partial x},{\partial\over \partial t}を含む微分演算子\right)f({x},{y})=g({x},{y}) \end{equation}のような微分方程式が与えられた時、これの解をいきなり探すのは難しい。そこで、この方程式の解が$f({x},{y})=X({x})Y({y})$のように${x}$を変数とする部分と${y}$を変数とする部分の積になるだろう、と仮定してみる。その後計算した結果、
\begin{equation} \left({\partial\over \partial x}と{x},X({x})の式\right) = \left({\partial\over \partial y}と{y},Y({y})の式\right) \end{equation}のように左辺と右辺に${x}$と${y}$が分離できたとする(これを「変数分離」と呼ぶ)。この式が成立するためには左辺も右辺も定数にならなくてはいけないので、その定数を$\alpha$と置いて、
\begin{equation} \left({\partial\over \partial x}と{x},X({x})の式\right)=\alpha,~~ \left({\partial\over \partial y}と{y},Y({y})の式\right)=\alpha \end{equation}という常微分方程式二つを解けばよい、というのが「偏微分方程式の変数分離」である。なお、変数分離で答が求まるというのはあくまで「仮定」であるから、これで正しい解が出ているかどうかについては注意しなくてはいけない。
$\alpha$は任意の定数だから、その定数に応じてたくさんの解が出るが、境界条件などにより実際の解がどのようになるかが決められることになる(このあたりは常微分方程式でもあったこと)。
特性曲線による解法
一例として、$\left({\partial\over \partial x}+a{\partial\over \partial y}\right)f({x},{y})=0$という微分方程式を考えよう。まず、
\begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right)(a{x}-{y})=0 \end{equation}であることはすぐわかる。実は任意の関数を$F$として、$F(a{x}-{y})$は、すべてこの方程式の解となる。
$F(a{x}-{y})$という関数は、$a{x}-{y}=C$($C$は定数)を満たす場所(つまり直線${y}=a{x}-C$上)では一定である。上で求めた解は、「直線${y}=a{x}-C$上で一定になる関数」だということになる。
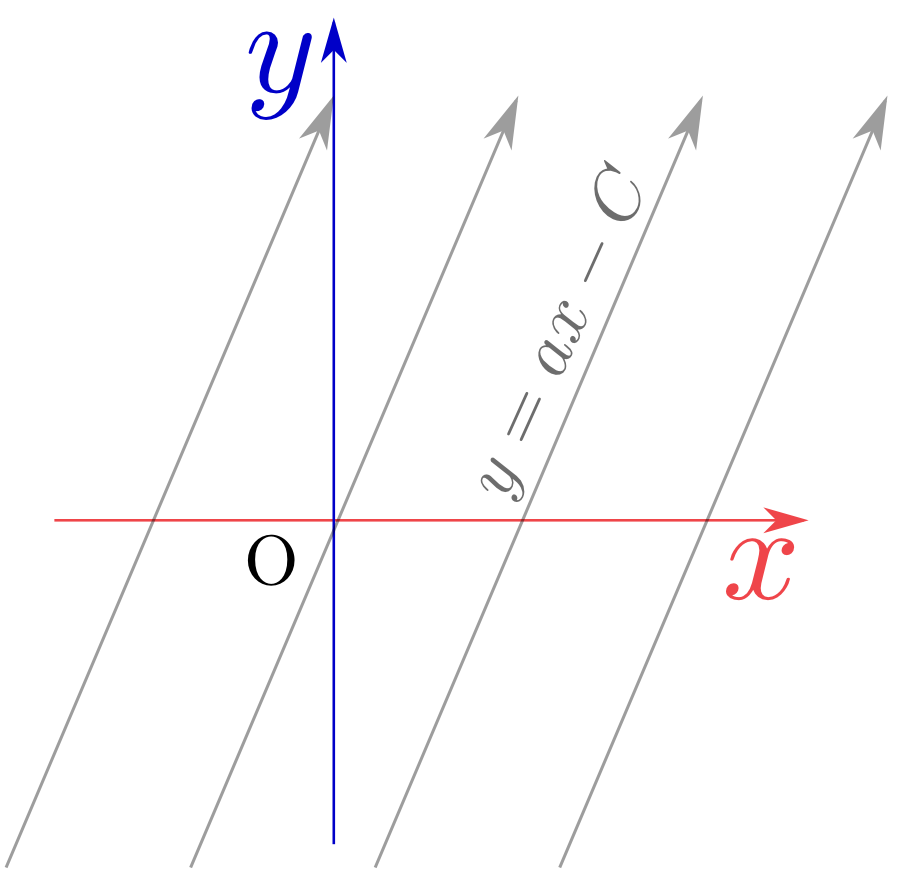
上の場合「直線」の上で解となる関数が一定となったが、
\begin{equation} \left( P({x},{y}){\partial\over \partial x} + Q({x},{y}){\partial\over \partial y} \right)f({x},{y})=0 \end{equation}のような偏微分方程式の場合、解である関数$\Phi({x},{y})$を一つ見つけることができたなら、任意の関数$F(t)$の$t$に$\Phi({x},{y})$を代入した$F(\Phi({x},{y}))$もやはり解となる。この場合は、$\Phi({x},{y})=C$(定数)であるような線(直線とは限らない)の上で$F$は一定となる。
たとえば、
\begin{equation} \left({\partial\over \partial x}+2{x}{\partial\over \partial y}\right)F({x},{y})=0 \end{equation}の解は、一つの解として${y}-{x}^2$を持つ(代入して確認せよ)。よって、$f$は任意の微分可能な関数とすれば、
\begin{equation} F({x},{y})=f({y}-{x}^2) \end{equation}が解となる。すなわち、${y}-{x}^2=(定数)$を満たす線($x=0$を軸とする放物線になる)の上で一定であるような関数なら全てこの微分方程式の解になる。
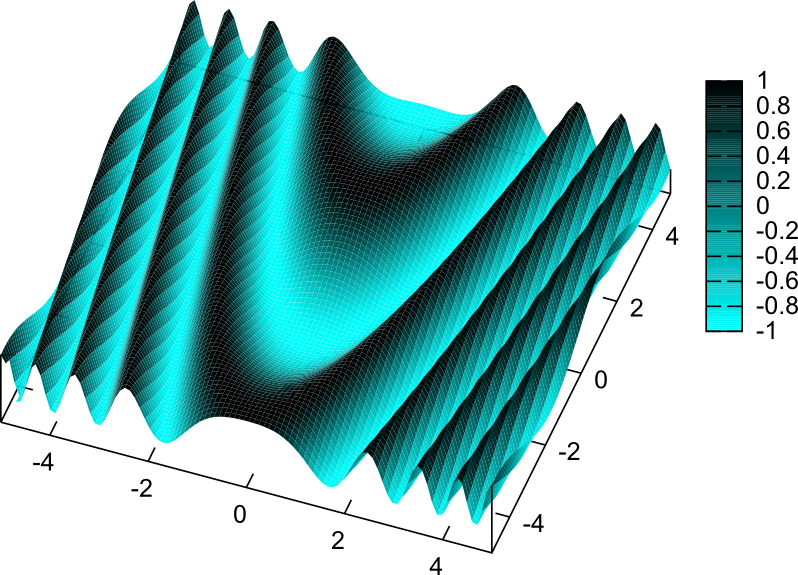
上の図は、$\sin(y-x^2)$のグラフである(放物線の上で一定になるような関数になっている)。
このような線を「特性曲線(charactaristic curve)」と呼ぶ。特性曲線を求めるということも、偏微分方程式の解法と言える。「偏微分には方向がある」ということを前の章で(少々くどく)述べたが、この節で述べた微分方程式の解き方は「偏微分が0になる方向を探す」という方針の解き方である。
「微分演算子の因数分解」による解法
常微分方程式の時に、
\begin{equation} \left( \left({\mathrm d\over\mathrm dx}\right)^2 +(a+b){\mathrm d\over\mathrm dx} +ab \right)f({x}) =\left({\mathrm d\over\mathrm dx}+a\right)\left({\mathrm d\over\mathrm dx}+b\right)f({x})=0 \end{equation}のように「微分演算子の因数分解」を行って解く方法があったことを思い出そう。この場合、解は$\left({\mathrm d\over\mathrm dx}+a\right)f({x})=0$の解である$\mathrm e^{-a{x}}$と、$\left({\mathrm d\over\mathrm dx}+b\right)f({x})=0$の解である$\mathrm e^{-b{x}}$の線型結合である$f({x})=C_a \mathrm e^{-a{x}}+C_b \mathrm e^{-b{x}}$になった。
同様にもし我々がたとえば偏微分方程式の微分演算子を \begin{equation} \left( \left({\partial\over \partial x}\right)^2 +(a+b){\partial^2\over \partial x\partial y} +ab\left({\partial\over \partial y}\right)^2 \right)f({x},{y}) =\left({\partial\over \partial x}+a{\partial\over \partial y}\right)\left({\partial\over \partial x}+b{\partial\over \partial y}\right)f({x},{y})=0 \end{equation}
のように`因数分解'して
\begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right) f({x},{y})=0 ~~または~~ \left({\partial\over \partial x}+b{\partial\over \partial y}\right)f({x},{y})=0 \end{equation}のように式を分離することができれば、問題を簡単化(二階微分方程式が一階微分方程式になった!)できる。
その他、常微分で使えたテクニック(たとえば線形であれば重ね合わせの原理が使える、など)の多くは偏微分方程式にも応用が効く。
以下の節では、代表的な「自然科学で現れる偏微分方程式」を解いてみよう。
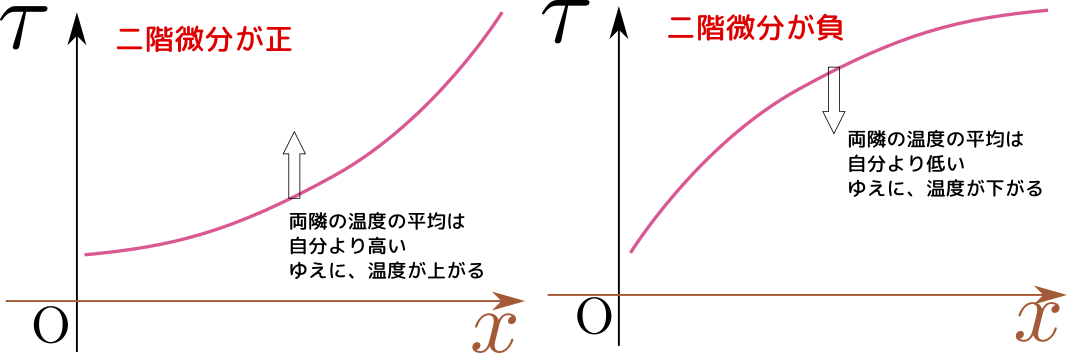
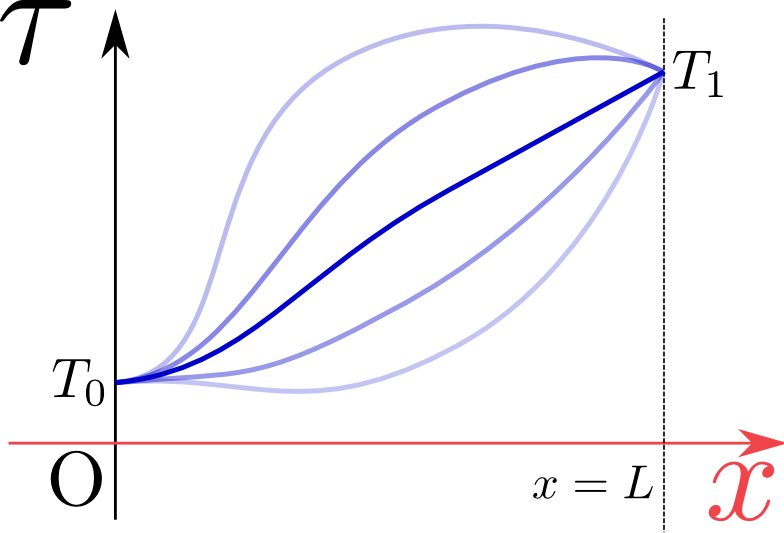 \begin{equation}
\begin{array}{rl}
\tau({t},{x}=0)&=T_0,\\[4mm] \tau({t},{x}=L)&=T_1
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rl}
\tau({t},{x}=0)&=T_0,\\[4mm] \tau({t},{x}=L)&=T_1
\end{array}
\end{equation}
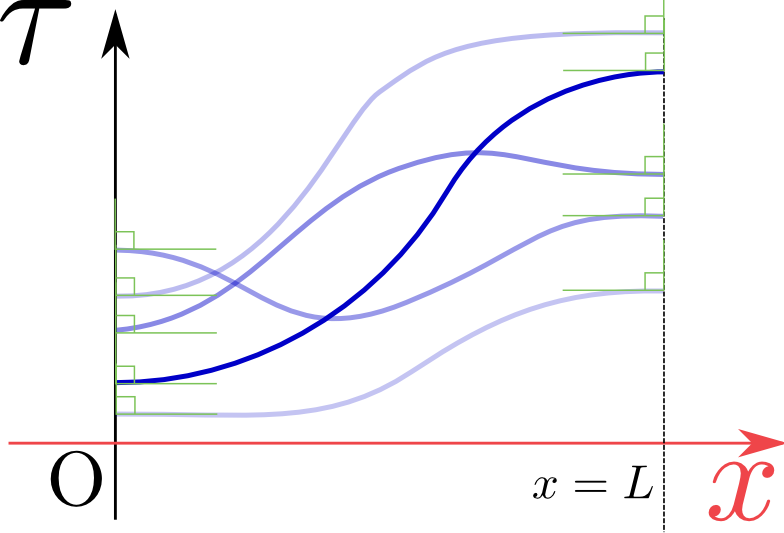 \begin{equation}
\begin{array}{rl}
{\partial \tau({t},{x})\over \partial x }\biggr|_{{x}=0}=&0,\\[4mm]
{\partial \tau({t},{x})\over \partial x }\biggr|_{{x}=L}=&0
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rl}
{\partial \tau({t},{x})\over \partial x }\biggr|_{{x}=0}=&0,\\[4mm]
{\partial \tau({t},{x})\over \partial x }\biggr|_{{x}=L}=&0
\end{array}
\end{equation}
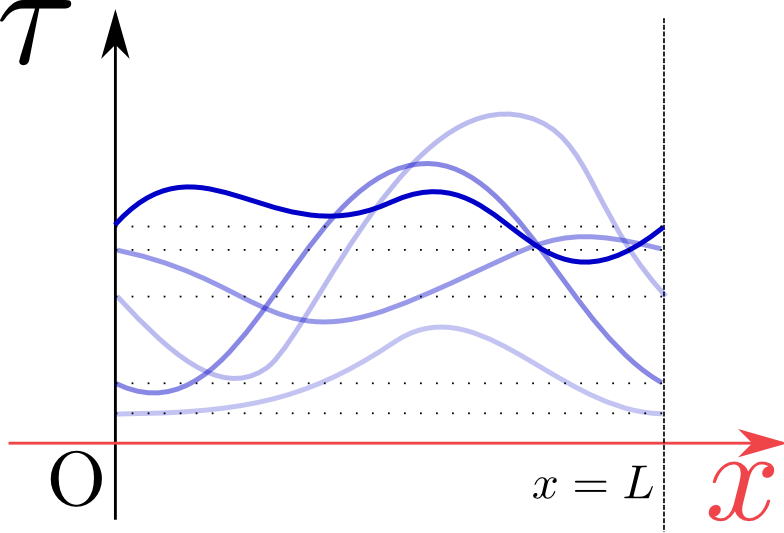 \begin{equation}
\begin{array}{rl}
\tau({t},{x}=0)=& \tau({t},{x}=L),\\[4mm]
{\partial \tau({t},{x})\over \partial x}\biggr|_{{x}=0}
=&
{\partial \tau({t},{x})\over \partial x}\biggr|_{{x}=L}
\end{array}
\end{equation}
\begin{equation}
\begin{array}{rl}
\tau({t},{x}=0)=& \tau({t},{x}=L),\\[4mm]
{\partial \tau({t},{x})\over \partial x}\biggr|_{{x}=0}
=&
{\partial \tau({t},{x})\over \partial x}\biggr|_{{x}=L}
\end{array}
\end{equation}