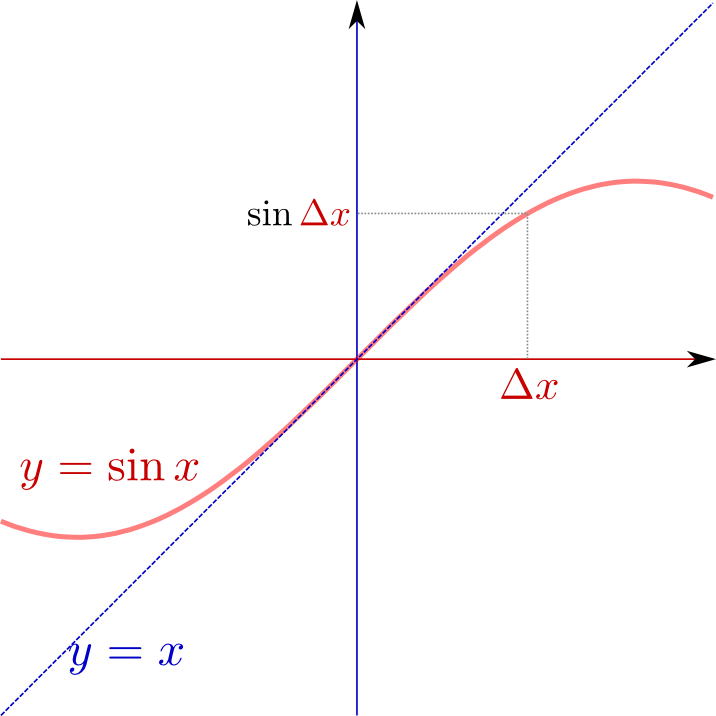

前にグラフで示した(しかしまだその根拠は示してない)ように、$\sin {x}$は${x}=0$付近では${x}$とほぼ同じ(傾き1)である。これは$\lim_{{\Delta x}\to0}{\sin{\Delta x}\over {\Delta x}}=1$ということである。同様に${x}$が小さいときに$\sin {x}\simeq {x}$であることは、電卓による計算で確認した。まずこれを図解で示そう。

上の図は半径1で中心角${\theta}$の扇型である。扇型の「弧」の部分の長さも${\theta}$となる(これはラジアンという角度の定義)。一方、$\sin{\theta}$というのは図に描かれた直角三角形の「高さ」に対応する。図には$\tan{\theta}$、すなわち「底辺1の直角三角形の高さ」も示した(後の都合で、「底辺」が上に来ている)。
ここでこの${\theta}$をどんどん小さくしていくところを想像して欲しい。当然、$\sin {\theta}$と$\tan{\theta}$も小さくなる(${\theta}\to0$の極限で全て0になるだろう)。
このとき、$\sin {\theta}<{\theta}<\tan{\theta}$という関係がある。それを示すには、$\sin{\theta},{\theta},\tan {\theta}$の三つは、図に示した三つの経路を伝わって点${\rm P}$から点${\rm Q}$、点${\rm Q'}$、点${\rm Q''}$へと向かう線(真ん中のだけは曲線で、残り2本は直線)の長さであることを使う。この三つの経路の中で、一番「まっすぐ」進んでいる${\rm P}\to {\rm Q}$が一番短く、もっとも「遠回り」している${\rm P}\to{\rm Q''}$が一番長い。
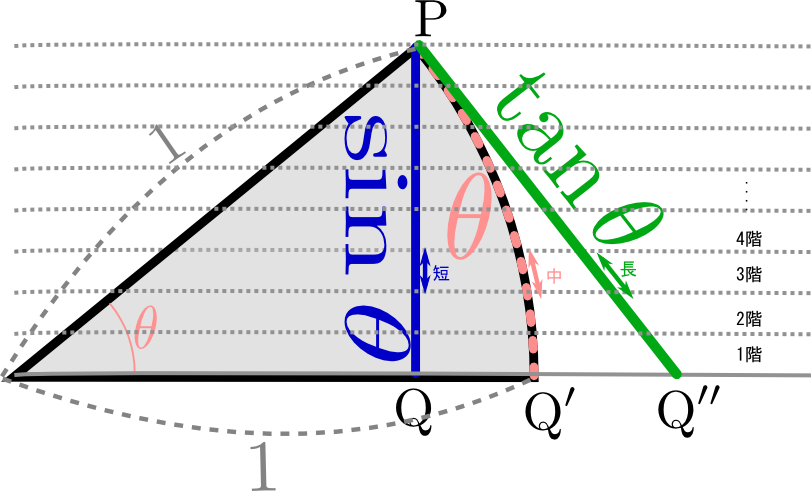
という説明で納得できない$\sin \theta$と$\tan\theta$の線は直線だが$\theta$の線だけ曲線なので長さの比較を直感に頼っていいの?と心配になるのは当然である。という人は右の図に点線で示したように、この三角形を$n$階建てのビルだと考えて厳密に長さを計算したいのであれば、この$n$を$n\to\infty$の極限を取ってという操作が必要になるかもしれないし、円弧であるところの長さを折れ線で近似するなどの作業も必要になるだろう。ここでは長短だけを判断できればよいので、この程度の議論でよしとしておく。、各々の階の部分での線の長さを考えよう。各階の高さを小さくすれば(つまり$n$階建ての$n$が無限に大きい極限を考えれば)全ての線はほぼ直線であるから、線の鉛直に対する傾きを見ることで、線の長さはここでなお、「{中}」とある線は、「ほんのちょっとだけ曲線」だから「長」より長かったりしないのか?---と不安になる人もいるかもしれないが、ここではそこは直感で乗り切ることにする。ちゃんとやるなら、「{中}」の線のふくらみ具合のオーダーを評価すれば、それが${\cal O}((階の高さ)^2)$だとわかる。

となるだろう。全体の長さは各階での長さの和だから、$\sin {\theta}<{\theta}<\tan{\theta}$が言える。
こうして得られた式$\sin {\theta}<{\theta}<\tan{\theta}$を${\theta}$で割ることで、
\begin{equation} {\sin {\theta}\over {\theta}}< 1 < \underbrace{{\sin {\theta}\over {\theta}}\times {1\over \cos {\theta}}}_{{\tan {\theta}\over {\theta}}} \end{equation}という式を作ることができて、さらにこの式の右側の部分である$1 < {\sin {\theta}\over {\theta}}\times {1\over \cos {\theta}}$に$\cos{\theta}$を掛けると$\cos {\theta}<{\sin {\theta}\over {\theta}}$が得られるから、
\begin{equation} \cos {\theta}< {\sin {\theta}\over {\theta}}< 1 \end{equation}が結論できる。この式を作ってから${\theta}\to0$という極限を取ると、$\cos {\theta}\to1$だから、間に挟まれた${\sin {\theta}\over {\theta}}$も1に近づく。これで$\lim_{{\theta}\to0}{\sin {\theta}\over {\theta}}=1$がわかった。
ここまででわかったことは、${\theta}$が小さい(0に近い)時は、
$\sin\theta$の近似式
\begin{equation} \sin {\theta}\fallingdotseq {\theta}~~~~~より正確には、 \sin {\theta}={\theta}+{\cal O}({\theta}^3) \end{equation}が使えることである。残りの部分が${\cal O}({\theta}^2)$ではなく${\cal O}({\theta}^3)$なのは、$\sin$が奇関数であること(つまり、$\sin (-{\theta})=-\sin {\theta}$であること)を知っているので、${\cal O}({\theta}^2)$はないからである。
では、$\cos{\theta}$の${\theta}$が小さいときの極限はどうなるだろう。$\cos0=1$であり、かつ$\cos$は偶関数($\cos (-{\theta})=\cos {\theta}$)だから、$\cos {\theta}=1+{\cal O}({\theta}^2)$であることがまずわかる。そこで、
\begin{equation} \cos {\theta}=1+a{\theta}^2+{\cal O}({\theta}^4) \end{equation}(残りの式が${\cal O}({\theta}^3)$ではなく${\cal O}({\theta}^4)$なのも、$\cos$が偶関数だから)として定数$a$を求めてみる。$\sin ^2{\theta}+\cos ^2{\theta}=1$に代入すると、
\begin{equation} \begin{array}{rl} \bigl( \underbrace{{\theta}+{\cal O}({{\theta}^3})}_{\sin {\theta}} \bigr)^2 +\bigl( \underbrace{1+a{\theta}^2+{\cal O}({{\theta}^4})}_{\cos {\theta}} \bigr)^2 =&1\\[5mm] {\theta}^2 + {\cal O}({\theta}^4)+1+2a{\theta}^2 + {\cal O}({\theta}^4)=&1 \end{array} \end{equation}となる${\theta}\times{\cal O}({\theta}^3)={\cal O}({\theta}^4)$のような計算をしている。が、右辺は1だから$a=-{1\over 2}$になって左辺の${\theta}^2$の係数が消えなくてはならず、
$\cos\theta$の近似式
\begin{equation} \cos {\theta}\fallingdotseq 1-{1\over 2}{\theta}^2~~~~~より正確には、 \cos {\theta}=1-{1\over 2}{\theta}^2+{\cal O}({\theta}^4) \end{equation}がわかる。
これらは今後もよく使う関係式である「覚えよう」とは言わない。何度も使うから覚えてしまうはずだ。これを「何度も使わない」としたら、勉強が足りない。。これを使って、三角関数の導関数を考えよう。
まず数式で考えていく。
三角関数の加法定理
\begin{equation} \sin (A+B)=\cos A\sin B+\sin A\cos B,~~ \cos (A+B)=\cos A\cos B-\sin A\sin B \end{equation}を使って
\begin{equation} \sin ({\theta}+\mathrm{d}\theta)=\cos {\theta} \sin \mathrm{d}\theta + \sin {\theta} \cos \mathrm{d}\theta \end{equation}という式を出す。ここで$\mathrm{d}\theta$は0に近づけるのだから${\cal O}(\mathrm{d}\theta^2)$は書かないことにすると、$\sin \mathrm{d}\theta =\mathrm{d}\theta$であり、$\cos\mathrm{d}\theta=1$であるから、
\begin{equation} \sin ({\theta}+\mathrm{d}\theta)= \sin {\theta}+\underbrace{\cos {\theta}}_{微係数}\mathrm{d}\theta \end{equation}となる($f({x}+\mathrm{d}x)=f({x})+f'({x})\mathrm{d}x$と比較せよ)。これから、
である。