物理学者によるタイムパラドックス分析

　物理学者がまじめにタイムマシンを考えた始めたのはそれほど最近ってわけでもないんだけど、やっぱり1988年にPhysical Review Lettersの６１巻1446ページに出たMorrisとThornとYurtserverの論文から後、議論が活発になったのは確かなようだ。この論文の中でどんなふうにタイムマシンが作られているのか、って話はとりあえずおいておいて（御用とお急ぎの方はThorn本人が書いている通俗書「ブラックホールと時空の歪み―アインシュタインのとんでもない遺産」（キップ・S. ソーン(著) 林一(訳)塚原周信(訳)あたりをご覧くださいまし）、ここでは物理学者がタイムパラドックスとどう戦ったかを書いていこう。

その１：Polchinskiのビリヤード

　タイムパラドックスと聞けばＳＦファンが一番最初に思い浮かぶのは親殺しのパラドックス。標準的なものとしては

という感じになりますわな。こういう話を聞いたら「結局タイムトラベラーは生まれるか生まれないのか、どっちやねん」と言いたくなるに違いない。ＳＦ作家たちもこれにいろんな解決を与えていて、

「俺の親　殺してみたら　他人（ひと）の親」というわけで、殺したけど自分の親は別人だった、ということにして問題ないことにしちゃったり、

「殺そうと　行ったつもりが　助けてた」というわけで、自分のタイムトラベルの結果、逆に死ぬはずだった親を助けてしまって逆につじつまがあっちゃったり、

「殺ったぜと　帰った先は　知らぬ場所」というわけで、自分が生まれないパラレルワールドに帰還しちゃったり、

「殺せない　ああ殺せない　殺せない」というわけで、どうやっても殺人が実行できなかったり、

まぁいろんなパターンで考えているもんです。物理学者がこのようなパラドックスを考える時、まず行うことは現象をできるだけ単純な（つまり計算することが可能な）モデルに置き換えちゃうこと。物理学者なんて連中は計算はできても人間の行動を予測するなんてことは不可能ですからな。馬券を買う時にもまず馬を球と近似して計算はじめるってぐらいなもんで。

　というわけで、Polchinskiのビリヤードというのは、この親殺しのパラドックスを計算可能な程度までモデル化しちゃったもの。
　まず、タイムマシンを用意する。そのタイムマシンは、図のように二つの穴でできていて、右の穴に入ると、左の穴から出てくる。ただし、左の穴から出てくる時刻は右の穴に入る時刻より前だとする。「そんなむちゃな」と言ってはいけない。タイムパラドックスの話をしているからにはタイムマシンができなくては話にならないんだから。まずはタイムマシンがあるところから始めるのである。
　この右の穴（以下「入り口」と呼ぶ）に赤いビリヤードの球を放り込む。そうすれば球が穴に入る「前」に左の穴（以下「出口」と呼ぶ）から出てくることになる。
　ここで入り口とか出口とか言ったが、このタイムマシンは双方向に移動できてもかまわないので、出口に入って入り口から出てきてもいい。ただしその場合は、出口に入ってからしばらく時間をおいて入り口から出てくるということになる。
　さて、この赤い球の入れ方をちょっと工夫してパラドックスが起こるようにしてみる。

　左の図のように、出口から出た球が最初にあった球と衝突するように、最初の球の速度と向きを調節するのである。入口に入った球がどれだけの時間前にどんな方向に飛び出てくるか、というデータをちゃんと知っていれば、うまく球が自分自身と衝突するようになげてやることが可能なはずだ。

　図をよく見ていただきたい。出口から出てきた球は、どこから来たのだろうか？

　「入口から入ったんだろ、そういう前提で計算したんだから」と言いたくなりますわな。

　ところが図をよく見るとわかるように、この球はもはや、入口に入らないのである。出口から出てきた自分自身によって進路を変えられてしまったからである。これで親殺しのパラドックスと同じようなパラドックスが発生していることがわかる。すなわち、

ということになるわけだ。念のためにここで強調しておこう。タイムパラドックスというのは、別に「自分で自分に衝突する」とか「自分の生まれる前の自分の親を殺す」ということ自体にあるのではない。もちろんこんなことは非常識であり、「原因は結果に先行する」という意味の因果律には反している。しかし、このこと自体はパラドックスではない。
　では何がパラドックスになるかというと、上に書いた（以下最初に戻る）で終わる文章をみるとわかるように、この問題には「じゃ、実際にはどういうことが起こるの？」という疑問に対するちゃんとした解がないようにみえるのである。
　物理学者は普通、初期状態が与えられるとそれにしたがって運動方程式をちまちまと解いていって問題の解をみつける。ところが、今考えた初期状態には、「こういう運動になる」という解が存在しないようにみえる。その「解がない」ということが問題なのであって、結果が原因に先行したって、それ自体は実は物理法則に反しない。だって、今の話の球自体の運動において、物理法則に反した部分はどこにもないではないか。ただ、その球が存在している空間にタイムマシンなんてものがいて（入口出口なんてものがあって）、時間的つながりが変になっているだけなのである。各点各点を取り出せば、どこにも物理法則が満たされていない場所はない。

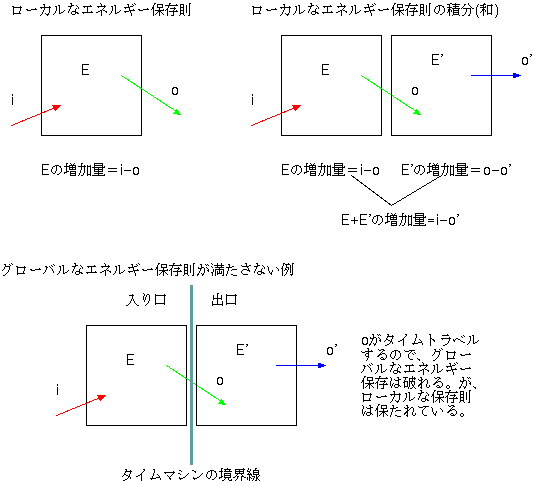　こう書くと「エネルギー保存則はどうなるの。１個だった球が２個に増えているけど」という疑問を持つ人がいるかもしれない。でもエネルギー保存則ってのは、ローカルなエネルギー保存則（具体的には、「ある場所のエネルギーは、そこから出ていった物体のエネルギーの分減り、そこに入ってきた物体のエネルギーの分増える」ということ）が先にあって、それを積分した（空間全部で足しあげた）結果できるものなのである。さっきの法則（赤字で書いたの）の中の「そこから出ていったもの」ってのはその隣にとっては「入ってきたもの」と同じだから、この出入りを全空間で足していくと、出たものと入ったものは等しくなり、全体として「エネルギーは増えたり減ったりしない」という法則（区別するために、こっちをグローバルなエネルギー保存則と呼ぼう）ができる。つまり、ローカルなエネルギー保存則の方がえらい法則なのである。となると今のようなタイムマシンがある場合、ナイーブに（ちなみに物理屋が「ナイーブに…する」と言ったら「やっちゃいけないことに気付かずに…しちゃう」という意味だ）考えるとエネルギー保存則が破れて見えるのは当然である。だって、「そこから出ていったもの」と隣に「入ったもの」を考える時、「入口」＝「そこ」、「出口」＝「隣」で考えると「出る」のと「入る」が同じ時刻じゃないのである（くどいようだがここで「そんなばかな」って言わないでくれ。タイムマシンの話してるんだから！）。だから単純に考えたらグローバルなエネルギー保存則が成立しないのはあたりまえ。でももっと大事な法則であるローカルなエネルギー保存則は成立しているのである。
　なお、この図の場合で言うと、出口からoというエネルギーが流れ込んできた時点で、グローバルなエネルギーはoだけ増えることになる。しかし入口にエネルギーoが流れ込む時点（これの方が、「出口からoというエネルギーが流れ込んできた時点」より後なのだ）でグローバルなエネルギーはoだけ減ることになり、全体として「o増えたエネルギーがo減った」ということで最終的収支は合う。

　さて、話をビリヤードに戻そう。Novikovその他の連中が、実際にこのビリヤードの問題をちゃんと数式を使ってごちゃごちゃと計算して、この問題には矛盾のない（consistent）解があることを見つけた。

　その解とは左の図のようなものだ。さっきの図ではCrash!!だった衝突が、Soft Touch.に変わっている。そのため、進路は少しだけ変わる。少しだけだったため、今度は少し速度は違うけども入口にちゃんと入る。そして入口に入ったのだから、それよりも前の時刻に出口から出てくる（出てきていた）。出てきた球は最初に予定していたのとちょっと違う進路を進み、自分自身に衝突する。ただし、Soft Touch.で。なんでCrash!!するように計算したはずなのに、Soft Touch.になるんだ、おかしいではないか、と思うかもしれない。その原因は、出口から出てきた球の進路が最初の予定と少し違っていたからである。なぜ進路が違っていたかというと、その前に未来から戻ってきた自分自身とSoft Touch.したからである。

　ほうら、物理学者は循環論法を使っている！と、ちよちゃん（誰のことかわからん人は例えばここをみてくれ）が言いそうだけど、すでに述べておいたように、今大事なのは原因と結果がどうこうという問題ではないのである。そんなものはタイムマシン使ったんだから崩れるに決まっているのだ。

　各点各点の物理法則はちゃんと満たして、かつ全体でも矛盾のない解があること。これが大事なのである。そして一見そういうものがなさそうに見えたビリヤード問題には、ちゃんと解があるのであった。上の図を見て、各点各点取り出して考える限り、どこにも物理法則を満たしてない場所がないことを確かめて欲しい。これは、ちゃんとした解なのである。

　これをいささか強引に親殺しのパラドックスにあてはめると、とどうなるか、と考えたんだけどうまくはまらないので、親殺しのパラドックスの簡易版である「自分殺しのパラドックス」（殺す相手が自分自身）で考えると、

とこうなる。いろいろ納得できない部分はあるだろうが、一応、筋は通っている。

その２：ビリヤードの解の唯一性

　今の話で、consistentな解がある、というところばかり強調した。では解は一個しかないのか、というのが次の問題になる。実は最初にNovikovたちが計算した時点で、解が二つあることはわかっていた。簡単に言うと、上の図で書いた「Soft Touch」が球（ってのは自分自身だが）を加速するようにタッチする場合と減速するようにタッチする場合があり得るのである。

　ところが後になって、実は解はもっとたくさんあることがわかった。ＳＦファンなら図を見れば即、「なあんだ、あれか」と思う、あれである。
　で説明を終わったら不親切なので、図にそって説明する。さあ実験するぞ、と赤い球を上に書いたような設定で打ち込むと、突然なぜか出口から青い球が現れるのである。そして青い球は赤い球に衝突する。そして赤い球はこの衝突の結果、入口に入れなくなる（ここまでは最初の設定と同じだ）。では青い球はどうなるかというと、跳ね返った結果、ちょうど入口に入るのである。では、入口に入った青い球はどこから出てくるか。それよりしばらく過去の出口である。ああっ、さっき青い球が出てきた理由はここにあったのか。

　話がうまくできすぎていると思うかもしれないが、実際問題としてこれにも矛盾はない。そしてこのような「存在の輪」解を解として認めてしまうと、青い球は別に白い球でもいいし、黒い球でもいい。カラスが飛んできてつっつくんでもいいし、元阪神の新庄が現われてさわやかに赤い球をジャンピングキャッチしてどこかに送球して、再び入口に消えたっていいわけだ。つまり、解は今度は事実上無限個あるということになるのである。

　さあ困った。解がないと困ってたはずなのに、今度は無限個ができてしまった。こうなると何が起こるか予測不可能、ということになってしまう。物理の世界というのはなんだかんだいいつつもたいてい決定論的で、初期値が決まればその後の運動がどうなるかは決まってしまうのが普通なのだが、この場合そうではない、ということが面白い。特にこの「存在の輪」解を認めない場合、赤い球の運動は非常に窮屈な、最初から決められた運動しかできない、という印象を与える。たとえば赤い球でなく人間だったとしたら、なんとかこの運命から逆らおうとするんじゃないのか、という疑問が生まれるに違いない。その点「存在の輪」解を認めてしまうと、赤い球の自由度はかなり広がるわけだ。実際に起こることがどれなのか決定できないというのは不安だ。将来タイムマシンを作った時に「突然新庄が現われてジャンピングキャッチするかも」と思いながら動作スイッチを入れなくてはいかんというのも困ったものである。

　さて、たくさんの解の可能性があるなら、いっそそのたくさんの可能性の重ね合わせ状態を考えたらどないだ、ということも考えられるわけで、量子力学で解いたらどないなるねん、ということになる。もちろんそういうことを考えた人はいて、たとえばH. David PolitzerがSimple quantum system in spacetimes with closed timelike curves(Phys. Rev. D46 4470)他の論文でビリヤード型とは別の簡単なタイムマシンの場合で量子力学を考えている。結果としてはこういう場合確率が保存しなくなる（通常の量子力学では保存する）こともあるようで、どうにも状況は不透明である。面白い話にはなりそうなのだが。

補足：Q&A

　上の内容について、いろいろとメールが来たので、それについて答えておこう。

　ごもっともな疑問である。(1)についてはわしが新庄なんていう例を出してしまったのが間違いかも。この「青い球」は別になんでもいいんだから、経年劣化しないようなものにしとけ、ということで納得してもらえるかなぁ？
　あるいはこの新庄はあの新庄とは全く関係ない新庄なので「自分がさっきまでしていたことをすっかり忘れることがある」という性格付けを与えてもよいかもしれぬ。
　ちなみに、SFではこういうのを「存在の環」と言うけど、その名前の通りのタイトルの短編小説では、その「存在の環」になっている物体にキズがついていて、「このキズはいったい誰がつけたんだ？」と悩む場面がありますな。

　なお、この「存在の環」の考え方については次のように切り返しが。

「存在の環」にはタイムパラドックスがあるのではないでしょうか。
絶対に劣化しない球となると韓非子の矛と盾みたいです。
物理的にあり得ない存在になるのではないでしょうか。

　これまたごもっともなのであるが、ここで紹介したビリヤード問題というのはある意味第１（第０？）近似みたいなもんであって、高校物理の問題で出てくる「回転が無視できる小球」とか、「まさつが無視できるなめらかな面」のように、「問題を簡単にするためのお約束」と、そういう意味でとらえるべきだと思う。
　もっともその点をどうしても心配するなら、量子力学的な存在で話をすればいいわけである。１粒子状態の散乱なんて考えると、粒子が不可弁別だから、下手すると赤い球と青い球すら区別不可能になってしまったりするわけだが。さらにこの方は

とまでおっしゃるのだが、こういう話は捨てる方向より、より拾う方向へ考えたほうが楽しいような気もするのだが。そもそもある意味思考のお遊びであり、お遊びがうまくいくように話を単純化しているわけであるから。

Polchinskiのビリヤードは矛盾のない解が導ける所にもっともらしさがあるのではないでしょうか。
もちろん、タイムトラベルが可能だという仮定の下で成り立つ解だから、タイムトラベルが不可能であった場合は荒唐無稽な御伽噺に過ぎません。
（そう考えると、本文のエネルギー保存即に関する記述は「前提事項を覆す反論は非論理的」の一言で済みますね。「前提事項を覆したらパラドックスを論じる意味がない」と言った方が文系には通じるかも知れません。）

劣化問題は微視的にはクリア出来る事例があるかも知れません。しかし、劣化問題は時間の矛盾によって発生する二次的問題であって、劣化しない球が存在しても時間の矛盾は解決できないはずです。青い球の滞在時間をtとして入口から登場する時刻を0とします。このとき入口から登場する青い球は時刻0の球です。そして、この球が次に出口に消える時刻はtとなります。とすると、次に入口から出てくる青い球は時刻tの球であるはずです。よって、青い球は時刻0の球であり、同時に時刻tの球であり・・・・同時に時刻n×tの球であることになります。今ここに居る私は今の私であり、同時に1年後の私でもあり、・・・同時にn年後の私でもある・・・わけがないですよね。これが本来起きているパラドックスであり、劣化問題はこのパラドックスが引き起こす見掛けの現象の一つに過ぎません。

　これが本来起きているパラドックスであると言うためには「経年変化」（この経年変化の中には、「人間の脳が何かを記憶する」なんてのも入っているわけである）のほかに「時間を測るもの」が存在していることになる。しかし、球に細かい構造がないという第０近似を行っている時に、「時刻０の球」と「時刻ｔの球」を弁別する方法は存在しないと思う。特に微視的な粒子を考えたとすると、陽子であれば「あっちの陽子」と「こっちの陽子」すら区別不可能なのである。

　このメールではさらに「たとえば、青い球が放射性同位体の原子ならば崩壊時間が無限大となる矛盾が生じます」などという指摘もいただいた。これは面白い問題なので深く考えてみたいところである。ある意味で「粒子」に最小の「構造」を持ち込んでいることになるので、「構造は持ち込む事で経年変化を具体化している」ということになるだろう。量子力学的に考える、という話はすでにあるが、さてそこに構造を持ち込んでいる場合はどうなるのか、そういう時も波動関数の形として無矛盾になっていれば問題はないわけであるが、問題あるという可能性は確かにある。なおこの方は最後に

　また、巨視的世界で適用できない解は実用上の意味を持たないことになります。さらに言えば、数学的に存在するのに現実には存在しない解もありえます。そう考えれば、青い球が微視的世界の特殊解として成り立っても、それが架空の解ではないとするだけの裏付けがありません。
　むしろ、時刻のパラドックスが生じることから架空の解である疑いが強いでしょう。

とおっしゃる。そりゃそうなのだが、こういう話は「とりあえずは第１近似としてこれでよかろう」と認めて、さらに先へと話を拡張できるかどうかと考える、というふうに前向きに考えた方が楽しいんじゃないかな、と思う。

次回予告：Krasnikovによる分析

↑のリンク先の論文で、Krasnikovという人がタイムパラドックスを物理的にはどう考えるべきか、という考察を行っている。彼の結論自体はちょっと首を傾げてしまう部分もあるんだけど、とりあえず分析のところは面白いので、この論文の内容にそって物理屋が考えるところのタイムパラドックスって何やねん、というところの話をもちっと突っ込んでみよう。