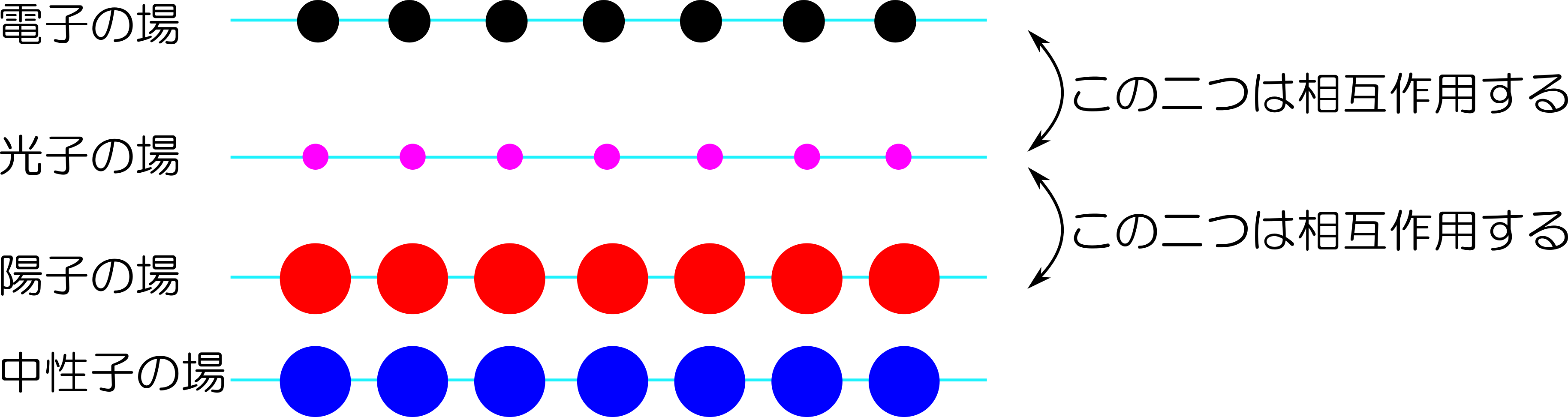
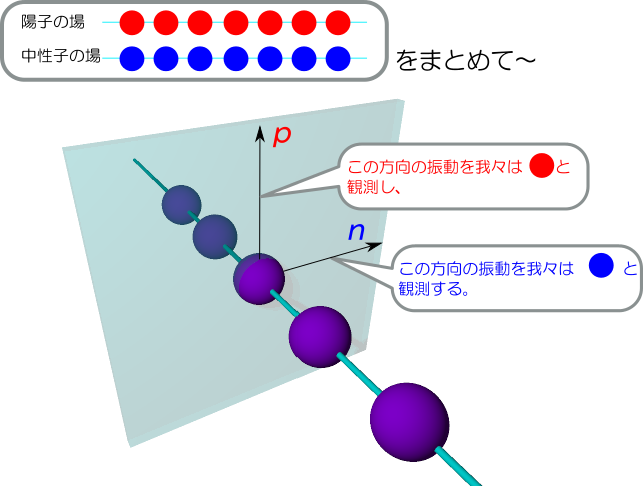
ちょっと質量が近いだけで、そんな(架空の方向での回転なんて)大それたことを考えてもいいのか?
と言いたくなるところですが、この「架空の空間の回転」理論(名前は「アイソスピン理論」と言います)は意外と(?)うまくいきました。素粒子物理学はその後理論も実験も発展を続けていき、素粒子の数もどんどん増えて、前に書いた
「物質」粒子の表
| u(アップ) | c(チャーム) | t(トップ) | 2e/3 |
|---|
| d(ダウン) | s(ストレンジ) | b(ボトム) | -e/3 |
|---|
| νe(電子ニュートリノ) | νμ(ミューニュートリノ) | ντ(タウニュートリノ) | 0 |
|---|
| e(電子) | μ(ミュー粒子) | τ(タウ粒子) | -e |
|---|
まで増えました(その一方で陽子や中性子は素粒子でなくなった)が、アイソスピン対称性は、
上2列の上下(u←→d、c←→s、t←→b)
と、
下2列の上下(νe←→e、νμ←→μ、ντ←→τ)
の対称性という形で残っているのです(電子にもアイソスピン対称性の相棒が見つかっていることに注意)。
ただし、実はこの表の素粒子には「左巻き成分」と「右巻き成分」というのがあり、アイソスピン対称性があるのは「左巻き成分」だけであって、「右巻き成分」には対称性はありません。ただこの話もやり始めると長い(そもそも左巻きって何?というのも説明がたいへん)ので、とりあえず右巻き成分というのは無視して考えます。これは素粒子の世界で左右対称性が最初っからない(最初あったのに破れたという話ではなく、最初っからない)という不思議な(面白い)話ではあるのですが。
表の一番右に電荷を書きましたが、上2段も下2段も「上下でeだけ電荷が違う」という点が共通しています。
さて、ここまで「質量の違いと電荷の違いに目をつぶれば対称性がある」と何度か言いました。こうなってくると、「ではこの違いを作ったのは何なのか?」という疑問も湧いてくるわけです。
Q:架空の方向の違いが粒子の種類の違いだとすると、波長とかの違いは何になりますか?
A:波長の違いは運動量の違いになります。
対称性をやぶった犯人は誰なのか? ---実はそれもヒッグス場なのです。