
★今年度の相対論の授業終わり
というわけで、最終回をリンクしとこう。
こっちは電磁気と違って、例年より速く進み、はじめて相対論的な電磁気学をゆっくりと話せた。原因は何かというと、今年から3年前期から3年後期に移動したことかもしれない。
やはり受けている学生も半年分成長していると、飲み込みがよくなっているのに違いない(と思うけど)。
珍しく最後までできたこともあって「F_μνの幾何学的意味は?」みたいな話までできた。というのは前々から「F_12=B_zって、z方向の磁場なのになんで添字は12なの?」みたいな疑問が出ることがあったのだが、この添字(12)は、
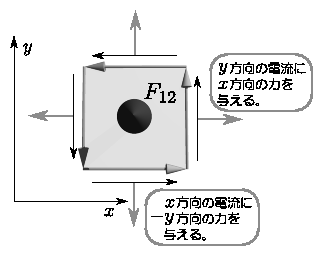
のような図を書いてあげると、「2方向の電流に1方向の力を与える」という意味で(12)なのだなぁ、とわかる、というわけ。
では当然次の質問として、「F_10はどうして添字(10)なのさ」ということになるわけだが、これも以下のような図を書くと、なんか納得できる。
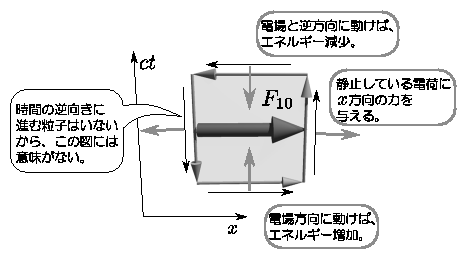
「時間方向の力」というのは、相対論では「仕事率」すなわち「エネルギーの増加率」になる(力=運動量の増加率だから、これでこそ相対論的)。
惜しいことに、この「時間方向の力」だけが向きが逆になってしまう(これは相対論だから時間成分にマイナスつくのはしょうがない)。
来年は担当外れたので、7年続けた相対論の講義も今日で終わりである。
★試験採点中
だいぶやさしくしたつもりだが、「マックスウェル方程式を書け」なんて言う、勉強してきた子にとっては
「キィーざます、ワタクシをなめないでもらいたいざます!」
と言いそうな問題も、できてないのがいるなぁ。
それよりも中間テスト欠席しといてしれっと期末テストに来ているのは何のつもりだ。
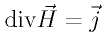 とか、なかなか見たことないマックスウェル方程式が出てきたぞ。
とか、なかなか見たことないマックスウェル方程式が出てきたぞ。
まぁできてないのはいつものことなのだが、今回選択問題の一つとして、
連続の式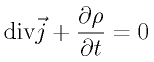 がマックスウェル方程式の中に含まれていることを示せ。
がマックスウェル方程式の中に含まれていることを示せ。
ってのを出しておいた(授業中この話はしておいたのだ)ら、なぜか、
「マックスウェルはアンペールの法則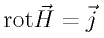 が矛盾を含むことに気づいた…」で始まる、例の変位電流の導出(「よくわかる電磁気学」なら278ページだ)をえんえんと書いている答案が続出。
が矛盾を含むことに気づいた…」で始まる、例の変位電流の導出(「よくわかる電磁気学」なら278ページだ)をえんえんと書いている答案が続出。
なんでそこまで戻って記述する必要がある??
こんなのはすでに知っている(そして問題にも出した)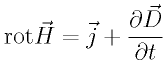 の両辺のdivとれば一発なのだが。
の両辺のdivとれば一発なのだが。
普通に解いた子(もちろん、ちゃんといました!)は3行で終わっている記述を、10行以上かかっている。しかも結論にたどり着かず、「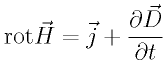 という式が導出されたのである」で終わっているのまでいる。
という式が導出されたのである」で終わっているのまでいる。
お前の目標点はそこじゃないだろ。
マックスウェルの話の筋書きは「連続の式が成り立つように、変位電流の項を入れる」なのだから、そもそも「連続の式が含まれていることを示せ」という問題と全くあっていないのである。
なんとなく「似た話を聞いたぞ」とサルベージされた記憶に飛びついてしまったんだろうな。入ってきた知識がまだまだ自分のものとして再構成されてないのだなぁ。まだまだ勉強足りませぬ。
自分が大学2年生の時を考えると、まぁしょうがないか。



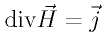 とか、なかなか見たことないマックスウェル方程式が出てきたぞ。
とか、なかなか見たことないマックスウェル方程式が出てきたぞ。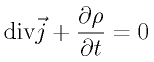 がマックスウェル方程式の中に含まれていることを示せ。
がマックスウェル方程式の中に含まれていることを示せ。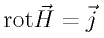 が矛盾を含むことに気づいた…」で始まる、例の変位電流の導出(「よくわかる電磁気学」なら278ページだ)をえんえんと書いている答案が続出。
が矛盾を含むことに気づいた…」で始まる、例の変位電流の導出(「よくわかる電磁気学」なら278ページだ)をえんえんと書いている答案が続出。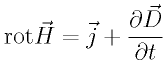 の両辺のdivとれば一発なのだが。
の両辺のdivとれば一発なのだが。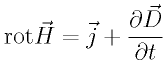 という式が導出されたのである」で終わっているのまでいる。
という式が導出されたのである」で終わっているのまでいる。