微分方程式の解に含まれるパラメータの数

上で述べたように、微分方程式には、微分方程式だけでは決まらないパラメータが必ず含まれる。それは微分方程式が局所的情報を表す式であることから必然的なのである。微分方程式を解く時にもこの点は大事なので、そのパラメータの数について考察しておこう。

$$\begin{equation} {{\mathrm d}y\over \mathrm d x} ={y}の解は~~~~~{y}=A\mathrm e^{{x}}\label{AEx} \end{equation}$$

を例として考えよう。このときのパラメータ$A$は

$$\begin{equation} \begin{array}{rll} {{\mathrm d}y \over \mathrm d x}=&{y}&({左辺に{y}を、右辺に{x}を集める}) \\ {{\mathrm d}y \over {y}}=&\mathrm d x&({両辺を積分})\\ \log{y}=&{x}+C \end{array}\label{solexbun} \end{equation}$$

の計算過程において${{\mathrm d}y\over {y}}=\mathrm d x$を積分するときの積分定数から現れたここで「両辺を${y}$で割る」という計算をやっているが${y}=0$の場合、これは許されない。ここでは暗黙のうちに${y}\neq0$を仮定している。と考えてよい。さらに、$\log{y}={x}+C$は

$$\begin{equation} {y}=\mathrm e^{{x}+C}=\mathrm e^C \mathrm e^{{x}} \end{equation}$$

となるから、$A=\mathrm e^C$とすれば上の式と同じになる「この形だと$A$は負になれないのでは？」と心配する人もいるかもしれないが、$C$が$\mathrm i\pi$という虚部を持っていれば、$A$は負にもなるので気にしなくてよい。。注釈に書いたように、ここまでの計算では${y}\neq0$が仮定されていたが、幸いなことに${y}=0$はこの一般解${y}=A\mathrm e^{{x}}$の、$A=0$の場合に含まれているので、${y}\neq0$の条件は外してよいことになる。

---

FAQ:左辺には積分定数はいらないのですか？

左辺に積分定数をつけても、結果は同じなのである。もし左辺に積分定数をつけたとすれば、左辺の積分定数と右辺の積分定数は別の定数なのでそれをそれぞれ$A,B$として時々、積分定数をどっちも$C$にして$\log{y}+C={{x}}+C$として両辺で打ち消してしまう、という計算をする人がいる（←ここは驚くか笑うかするところ）が、積分定数は左辺と右辺それぞれにおいて「任意の数」だから、両辺で一致する理由はない。

$$\begin{equation} \begin{array}{rl} \log{y}+A=&{{x}}+B\\[3mm] \log{y}=&{{x}}+B-A \end{array} \end{equation}$$

となるが、$A$も$B$もまだ決まっていない数であり、しかも結果には$B-A$という組み合わせでしか出てこない。つまり、答えを出すためには$A,B$それぞれを求める必要はなく、$B-A$だけを求めればよいから、$C=B-A$とおいて１つの積分定数と思えばよい。

---

非常に簡単な二階微分方程式$\left({\mathrm d\over\mathrm dx}\right)^2f({x})={\mathrm d\over\mathrm dx} f({x})$を同様に解いてみよう。

$$\begin{equation} \begin{array}{rll} \left({\mathrm d\over\mathrm dx}\right)^2f({x})=&{\mathrm d\over\mathrm dx} f({x}) &({両辺を不定積分}) \\ {\mathrm d\over\mathrm dx} f({x})=&f({x})+C&({f({x})+C={y}と置く})\\ {\mathrm d\over\mathrm dx} ({y}-C)=& {y}&({{\mathrm d\over\mathrm dx}(-C)=0を使って、さらに変数分離})\\ {{\mathrm d}y\over {y}}=& \mathrm d x&({もう一度積分})\\ \log {y}=& {x}+D&({\mathrm e の肩に乗せて})\\ {y}=&\mathrm e^{{x}+D}&({f({x})に戻して})\\ f({x})=& -C + \mathrm e^{{x}+D} \end{array} \end{equation}$$

積分を二度やったため、積分定数$C,D$の二つが結果に現れる（パラメータの数は2）。

微分方程式を解くとは積分すること、と考えると「$n$階微分方程式なら不定積分を$n$回繰り返せば解ける」と言えて、結果は$n$個の積分変数を含む。上の具体例を見ると、確かに一階微分方程式の解は1個の、二階微分方程式の解は2個の積分定数を含んでいる。

結論として、$n$階微分方程式の解は常に$n$個の「微分方程式だけでは決まらないパラメータ」を含んでいることになるただし、${1\over {x}}$の積分のところで示したように、途中で関数が定義できない点（この例の場合${x}=0$）があると積分一つに対して二個の積分定数が出て来ることもあるので、そのような場合には注意が必要である。。

こういう考え方もできる。解析的な関数（つまり、テイラー展開できる関数）に限って考えると、「関数を決める」というのは、

$$\begin{equation} f({x})=\sum_{n=0}^\infty {1\over n!}f^{(n)}(x_0)({x}-x_0)^n \end{equation}$$

の係数$f^{(n)}(x_0)$を全て決めることである（少なくともテイラー展開の収束半径の内側ではこれで十分である）。

$m$階微分方程式は（適切な変更を行った後）

$$\begin{equation} f^{(m)}({x})= \biggl(f^{(m-1)}({x}),f^{(m-2)}({x}),\cdots,f^{(1)}({x}),f^{(0)}({x})\biggr)の式 \end{equation}$$

のように書くことができる。さらにこれをどんどん微分することで、

$$\begin{equation} \begin{array}{rll} f^{(m+1)}({x})=& \biggl(\underbrace{f^{(m)}({x})}_{微分方程式を代入},f^{(m-1)}({x}),f^{(m-2)}({x}),\cdots,f^{(1)}({x}),f^{(0)}({x})\biggr)の式\\ =& \biggl(f^{(m-1)}({x}),f^{(m-2)}({x}),\cdots,f^{(1)}({x}),f^{(0)}({x})\biggr)の式\\ \end{array} \end{equation}$$

のように$m$階より高い階数の微係数も求めることができる。これらを使って$f^{(m)}(x_0)$をそれより微分階数の低い係数と使って書き直すことができるから、$f({x})$の表現には、$m$より低い階数の微係数$\left(f^{(m-1)}(x_0),f^{(m-2)}(x_0),\cdots,f^{(1)}(x_0),f^{(0)}(x_0)\right)$だけが「決まらずに」残る。

たとえば一階微分方程式を満足する関数であれば$f(x_0)$のみが、二階微分方程式を満足する関数であれば$f(x_0)$と$f'(x_0)$の二つだけが微分方程式だけでは決まらないパラメータとなる。

一階微分方程式で正規形の場合で、「決まらないパラメータ」の意味を考えておこう。

${{\mathrm d}y\over \mathrm d x}=f({x},{y})$という式が与えられていると、${x}$-${y}$平面上である点$({x},{y})$を指定すると、その点における関数のグラフの傾き${{\mathrm d}y\over \mathrm d x}$がわかる、という式になっている。つまり、${{\mathrm d}y\over \mathrm d x}=f({x},{y})$という式は、各点各点において「グラフの線はどちらに伸ばすべきか」を与えている。

たとえば最初に考えた微分方程式は${{\mathrm d}y\over \mathrm d x}={y}$と書けるが、その解のグラフは、各場所において${y}$座標と同じ傾きを持っている曲線である。

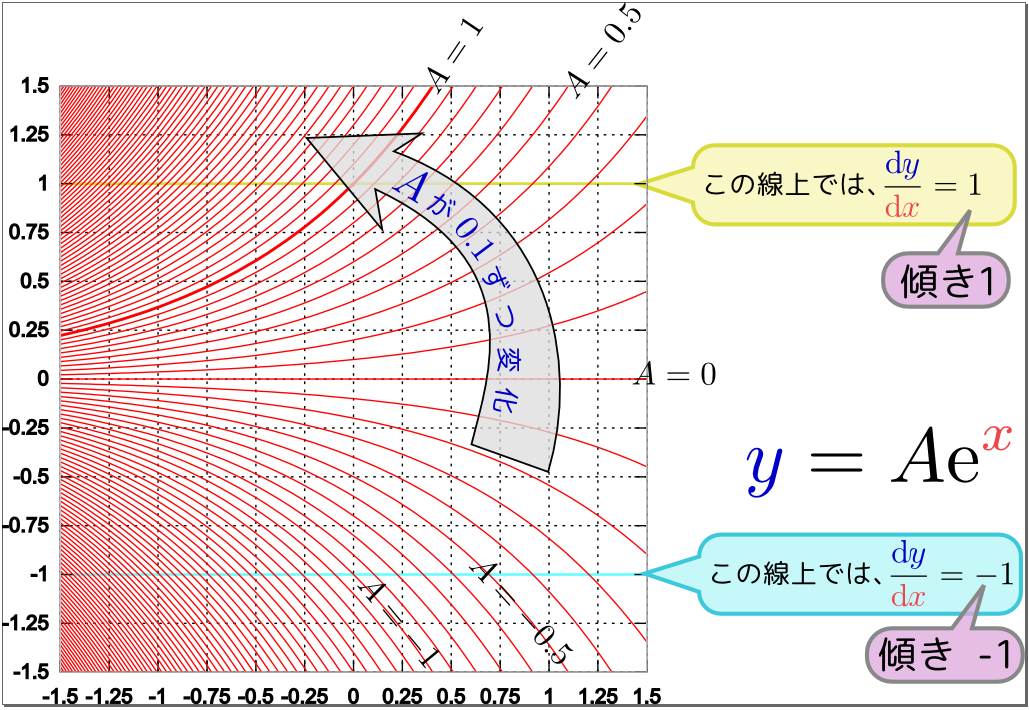
そういう曲線を次々と描いていくと、上のグラフにあるように全平面を埋め尽くしていく。

たとえば${x}=0$の時${y}=1$というふうに「出発点」を決めると、この場合は${y}=\mathrm e^{{x}}$という線（グラフでは１本だけ太い線で表現した）の上を進んでいくことになる。

一階微分方程式が指定するのは傾きのみであるから、出発点（上の例では${x}=0$から始めたが、実はどの場所でもよい）を指定すれば曲線は一つ決まる。別の点を出発点にすれば（たまたま同じ線上の２点を選ばない限り）また別の線が引ける。こうして、微分方程式だけからは決まらないパラメータが解には入っていることになる（後で、それを「初期条件」などで決めていく方法について述べる）。

二階微分方程式では、傾きではなく「曲がり具合」が微分方程式によって指定され、「場所」と「傾き」が微分方程式では決まらない量になる。

変数分離できる一階微分方程式

まず微分方程式がどういうものかに慣れることが必要だと思うので、以下では、微分方程式の中でも比較的簡単（でも応用範囲は広い）な「変数分離できる一階微分方程式」の具体例を考えていこう。

変数分離はいつでもできるとは限らないことに注意しよう。たとえば${\mathrm dy\over \mathrm dx}({x})={x}+{y}$という簡単な場合でも左辺に${y}$だけを集めることはできない（この微分方程式は解ける。つまり変数分離できなくても解ける時は解ける）。

以下この節では「変数分離できる場合」に限って話をする。

例として上げた${{\mathrm d}y\over \mathrm d x}={y}$は変数分離できる微分方程式の例でもある。上でやったように、「変数分離した後で積分」という方法で解くことができた。

もう一つ、簡単な例を示そう。

$$\begin{equation} {{\mathrm d}y\over \mathrm d x}=-{{x}\over {y}} \end{equation}$$

という式（前に図で考えた微分方程式で、答は円であった）は書き直すと${y}{\mathrm d}y = -{x} \mathrm d x$と変数分離できる。これを積分すると、

$$\begin{equation} \begin{array}{rl} \int {y}{\mathrm d}y =& -\int{x} \mathrm d x\\[3mm] {{y}^2\over 2}=&-{{x}^2\over 2}+C \end{array} \end{equation}$$

となる。$C$は積分定数である。結果を整理すると、

$$\begin{equation} {x}^2 +{y}^2 = 2C \end{equation}$$

という円の式が出てくる（半径は$\sqrt{2C}$である）。

次に${{\mathrm d}y\over \mathrm d x}={{y}\over {x}}$を同様に解いてみよう（図で考えた時、この解は「原点を通る直線」であった）。まず変数分離して、

$$\begin{equation} \begin{array}{rll} {{\mathrm d}y\over {y}}=&{\mathrm d x\over {x}}&({積分})\\ \log {y} =& \log {x} +C&({両辺を\mathrm e の肩へ})\\ {y}=& {x}\mathrm e^C \end{array} \end{equation}$$

となり、確かに（傾き$\mathrm e^C$の）直線が解である（図を描いて考える方がすっとわかる）。