指数関数${y}=a^{{x}}$を微分することを考えよう。まずは数式で「微分の定義」までちゃんと戻って考える。実は$a=\mathrm e$の時が一番簡単なので、まずはその場合を考えよう。
\begin{equation} {\mathrm d \over \mathrm dx }\left(\mathrm e^{x}\right)= \lim_{{\Delta x}\to0}{\mathrm e^{{x}+{\Delta x}}-\mathrm e^{x}\over {\Delta x}} =\mathrm e^{x} \times\lim_{{\Delta x}\to0}{\mathrm e^{{\Delta x}}-1\over {\Delta x}} \end{equation}のように、極限の式から$\mathrm e^x$を外に出してしまう。こんなふうに外に出てしまうのは、指数関数という関数が「${x}$が${\Delta x}$増加すると「元の値」の$\mathrm e^{{\Delta x}}$倍になる」という性質を持っている(ということはつまり、増加量も元の関数の値に比例する)ということの顕れである。
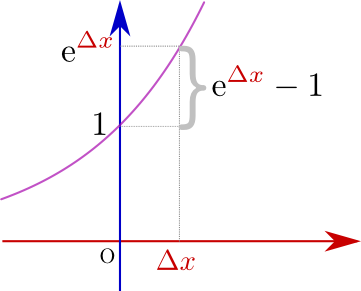
残った部分$\lim_{{\Delta x}\to0}{\mathrm e^{{\Delta x}}-1\over {\Delta x}}$はよく見ると${x}$によらない定数になっている。そしてこれは、${y}=\mathrm e^{x}$の${x}=0$での傾きそのものである(右のグラフ参照)。そしてそれは$\mathrm e$の定義により1である。つまり、
\begin{equation} {\mathrm d \over \mathrm dx }\left( \mathrm e^{{x}}\right)=\mathrm e^{x}\label{expbibun} \end{equation}なのである。$\mathrm e^x$という関数は「微分しても変わらない関数」であった、ということがわかる(だから$\mathrm e$は重要なのである)。
「微分しても変わらない関数ってどんなもの?」という視点から、指数関数を「導いて」みよう。まず我々は$\mathrm e^{{x}}$の${x}=0$での値が1で傾きが1であること、つまり${x}=0$の近傍では$\mathrm e^{x}=1+{x}$であることを知っている。しかし、$1+{x}$を微分すると
\begin{equation} {\mathrm d \over \mathrm dx }\left(1+{x}\right)\stackrel{?}{=}1 \end{equation}となって元に戻らない。微分した後に${x}$がいるためには、関数に${1\over 2}{x}^2$を加えておくとよいだろう。しかし、
\begin{equation} {\mathrm d \over \mathrm dx }\left(1+{x}+{1\over 2}{x}^2\right)\stackrel{?}{=}1+{x} \end{equation}であるからこれでは微分すると(右辺に${1\over 2}{x}^2$が足りない分)元に戻らない。ではということでさらに${1\over 2\times3}{x}^3$を加える。すると、
\begin{equation} {\mathrm d \over \mathrm dx }\left(1+{x}+{1\over 2}{x}^2+{1\over 2\times3}{x}^3\right)\stackrel{?}{=}1+{x}+{1\over 2}{x}^2 \end{equation}となる。この手順を繰り返していくと考えれば、
\begin{equation} \begin{array}{rl} \mathrm e^{{x}}=&1+{x}+{1\over 2}{x}^2+{1\over 2\times3}{x}^3 +{1\over 2\times 3\times 4}{x}^4+{1\over 2\times 3\times 4\times 5}{x}^5 +\cdots\\ =&\sum_{n=0}^\infty {1\over n!}{x}^n \end{array} \end{equation}という無限につづく項の和で書ける、ということになる。前に$1+1+{1\over2}+{1\over 2\times3}+{1\over 2\times 3\times 4}+{1\over 2\times 3\times4\times 5}+\cdot$という計算で$\mathrm e$が出せる、という話をしたが、その理由はこれである。
次に$\mathrm e^{kx}$のように指数が定数$k$倍されている場合を考えると、
\begin{equation} {\mathrm d (\mathrm e^{kx})\over \mathrm dx }= \lim_{{\Delta x}\to0}{\mathrm e^{kx+k{\Delta x}}-\mathrm e^{kx}\over {\Delta x}} =\mathrm e^{kx}\lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {\Delta x}} \end{equation}となるが、
\begin{equation} \lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {\Delta x}}= \lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {k{\Delta x}\over k}} = k\lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {k{\Delta x}}} \end{equation}としてから$k{\Delta x}=t$と置くとこの式はさらに$k\lim_{t\to0}{\mathrm e^{t}-1\over {t}}$と書き直せて、この極限は$k$だから、
\begin{equation} {\mathrm d (\mathrm e^{kx})\over \mathrm dx }= k\mathrm e^{kx} \end{equation}となる(このような状況を「$k$が$\exp$の肩から降りてくる」と表現する)。
ここまでくると、底が$\mathrm e$ではなく一般の正の数であった場合も同様に、$a=\mathrm e^{\log a}$と書けることを使って$a^{{\Delta x}}=\mathrm e^{{\Delta x} \log a}$と直して考えて、
がわかる($a=\mathrm e$なら、$\log\mathrm e=1$だから${\mathrm d (\mathrm e^x)\over \mathrm dx }= \mathrm e^x$に戻る)。
${y}=\log{x}$を微分するには、まず$\mathrm e^{y}={x}$として、
\begin{equation} \begin{array}{rl} \mathrm e^{y}=&{x} \\ \underbrace{\mathrm e^{y}}_{{x}}\mathrm dy =&\mathrm dx \\ {\mathrm dy \over \mathrm dx }=& {1\over {x}} \end{array} \end{equation}とすればよい(もちろん、$\mathrm e^{{x}}$の逆関数だから${1\over \mathrm e^{{x}}}$になると考えてもよい)。
前に、${x}^\alpha$のような冪の形で、微分して${1\over {x}}$になる関数はない、という話をしたが、$\log{x}$というのがそういう関数になる。
この式と合成関数の微分則から、$\log \left(f({x})\right)$の微分は
\begin{equation} {\mathrm d \over \mathrm dx }\log \left(f({x})\right) =f'({x})\times {\mathrm d \over \mathrm df}\log|f|= {f'({x})\over f({x})} \end{equation}となる。これから、
\begin{equation} f'({x})= f({x})\times {\mathrm d \over \mathrm dx }\log \left(f({x})\right) \end{equation}のように微分の計算を行うことができる(つまり、$\log$を取ってから微分して元の関数を掛けることで微分ができる)。
ややこしくなりそうに思うかもしれないが、対数の性質のおかげでこれで楽ができる状況もある。というのは、関数の積$f({x})g({x})$の微分はライプニッツ則を使うと、
\begin{equation} {\mathrm d \over \mathrm dx }\log \left(f({x})g({x})\right)={\overbrace{f'({x})g({x})+f({x})g'({x})}^{(f({x})g({x}))'}\over f({x})g({x})}\label{taisuubibunkihon} \end{equation}積の対数が対数の和になることを使うと
\begin{equation} {\mathrm d \over \mathrm dx }\log \left(f({x})g({x})\right)= {\mathrm d \over \mathrm dx }\log \left(f({x})\right) + {\mathrm d \over \mathrm dx }\log \left(g({x})\right)={f'({x})\over f({x})} +{g'({x})\over g({x})} \end{equation}となり、この二つは(当たり前だが)一致する。これを使うと、複雑な掛算があるときに各々の因子の微分を別々に行うことができるのである。また、分数関数の微分も、
\begin{equation} {\mathrm d \over \mathrm dx }\log \left({f({x})\over g({x})}\right)= {\mathrm d \over \mathrm dx }\log \left(f({x})\right) - {\mathrm d \over \mathrm dx }\log \left(g({x})\right)={f'({x})\over f({x})} -{g'({x})\over g({x})} \end{equation}のように$\log$を取った後では符号の違いのみとなり、
\begin{equation} {\mathrm d \over \mathrm dx }\left({f({x})\over g({x})}\right)=\left({f({x})\over g({x})}\right) \times {\mathrm d \over \mathrm dx }\log \left({f({x})\over g({x})}\right) =\left({f({x})\over g({x})}\right) \times\left( {f'({x})\over f({x})} -{g'({x})\over g({x})}\right) \end{equation}という計算もできる。
また、${y}={x}^{{x}}$のようなややこしい冪で表された関数も、対数を取ってから微分する方法が楽である。
\begin{equation} {\mathrm d \over \mathrm dx }\left(\log{x}^{{x}} \right) ={\mathrm d \over \mathrm dx }\left( {x}\log{x} \right) =\log{x}+{x}\times {1\over {x}}=\log{x}+1 \end{equation}のように微分して、
\begin{equation} {\mathrm d \over \mathrm dx }{x}^{{x}}={x}^{{x}}\times \left(\log{x}+1\right) \end{equation}とする。
という式がよく使われる(この二つの式は互いに逆関数になるという関係でつながっている)。
ない。なぜなら$\log 0$は定義されていない量(無理矢理書くなら$-\infty$)だからである。
導関数$f'({x})=\lim_{{\Delta x}\to0}{f({x}+{\Delta x})-f({x})\over {\Delta x}}$の導関数、つまり
\begin{equation} f''({x})=\lim_{{\Delta x}\to0}{f'({x}+{\Delta x})-f'({x})\over {\Delta x}} \end{equation}を作ってみよう。これを「二階微分」非常に頻繁に「二回微分」と書く人がいるが、これは誤字である(しかし発音では区別がつかないから安心だ)。と呼び、記号としては$'$を重ねて$f''({x})$と表現することにしよう($f({x})\to f'({x})$が「一階微分」、$f({x})\to f'({x})\to f''({x})$が「二階微分」である)。また、一階微分を${\mathrm d \over \mathrm dx }f({x})$と書いたように、二階微分は
\begin{equation} f''({x})= {\mathrm d \over \mathrm dx }\left( {\mathrm d \over \mathrm dx }f({x}) \right)= {\mathrm d ^2\over \mathrm dx ^2} f({x})={\mathrm d^2 f\over \mathrm dx ^2}({x})\label{nikai} \end{equation}と表現してもよい。
同様に三階微分や四階微分も定義されるが、数が大きくなった時は(十階微分を$f^{\prime\prime\prime\prime\prime\prime\prime\prime\prime\prime}({x})$などと書くのは不経済なので)$n$階微分は$f^{(n)}({x})$と表現する$\left(f''({x})={\mathrm d ^2\over \mathrm dx ^2}f({x})=f^{(2)}({x})\right)$。
二階微分がどんな意味を持つかを考えよう。二次関数や三次関数の形を考えたときに、1次の項${x}$の係数が原点における傾きを、2次の項${x}^2$の係数が原点における「曲がり具合」を表現していたのを覚えているだろうか。その考え方からすると、二階微分の値は「曲線の曲がり具合」を表現することになる。
定義式から二階微分を計算することで、確かに「曲がり具合」であることを確認しよう。まず、$ f''({x})=\lim_{{\Delta x}\to0}{f'({x}+{\Delta x})-f'({x})\over {\Delta x}}$という二階微分の意味を表した式そのものに、一階微分の式$\lim_{{\delta x}\to0}{f({x}+{\delta x})-f({x})\over {\delta x}}$を代入する(ここで、二つの極限は別のものなので、一階微分の方はいつもの${\Delta x}$ではなく${\delta x}$という記号を用いた)。すると、
\begin{equation} \begin{array}{rll} f''({x}) =&\lim_{{\Delta x}\to0}{\overbrace{ \lim_{{\delta x}\to0}{f({x}+{\Delta x}+{\delta x})-f({x}+{\Delta x})\over {\delta x}}}^{f'({x}+{\Delta x})} -\overbrace{\lim_{{\delta x}\to0}{f({x}+{\delta x})-f({x})\over {\delta x}}}^{f'({x})} \over {\Delta x} } \\[3mm] =&\lim_{{\Delta x}\to0}\lim_{{\delta x}\to0} {\left( f({x}+{\Delta x}+{\delta x})-f({x}+{\Delta x})\right) -\left( f({x}+{\delta x})-f({x})\right) \over {\Delta x}{\delta x} } \end{array} \end{equation}という式が出る。
ここで二つの極限${\Delta x}\to0$と${\delta x}\to0$を行わなくてはいけないのだが、どちらも0にするという点では同じなので、この二つの極限を同時に取ることにする。そこで${\delta x}={\Delta x}$と置いて極限の記号を一つにして書き直すと、
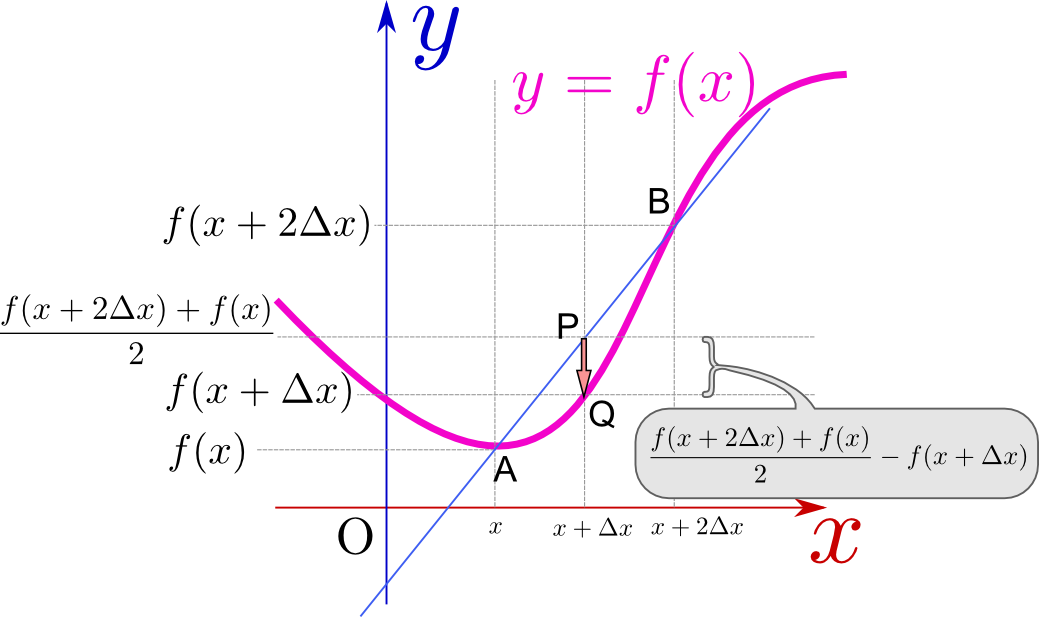
\begin{equation} \begin{array}{rll} f''({x}) =&\lim_{{\Delta x}\to0}{\left( f({x}+2{\Delta x})-f({x}+{\Delta x})\right) -\left( f({x}+{\Delta x})-f({x})\right) \over ({\Delta x})^2 } \\ =&\lim_{{\Delta x}\to0}{ f({x}+2{\Delta x})-2f({x}+{\Delta x}) +f({x}) \over ({\Delta x})^2 }\\ =&2\lim_{{\Delta x}\to0}{ { f({x}+2{\Delta x}) +f({x})\over 2} -f({x}+{\Delta x}) \over ({\Delta x})^2 } \end{array}\label{nikaibibunteigi} \end{equation}という計算になる。最後で2を前に出したのは、分子の${f({x}+2{\Delta x})+f({x})\over 2}-f({x}+{\Delta x})$に図形的意味があるからである。
その意味するところを説明しよう。下のグラフを見て欲しい。

図の点Pは点A$({x},f({x}))$と点B$({x}+2{\Delta x},f({x}+2{\Delta x}))$の中点であり、その高さが${f({x}+2{\Delta x})+f({x})\over 2}$である。
一方$f({x}+{\Delta x})$は点Qの高さである。つまり、点Aと点Bの中点に比べて、点Qがどれだけ下がっているか、という量であり、これは「線の曲がり具合」を表現している。二階微分の値は「両隣の平均に比べて自分がどれだけ下がっているか」を示す量だとも言える。

それは上の図に示したように「上に凸か下に凸か」を表す量にもなっている。
自然において、二階微分が正なら増加し、二階微分が負なら減るという傾向を持つ現象がたくさんある(後で、微分方程式でこれを表現するとどうなるか、ということを示そう)。これはつまり、下に凸なら増加、上に凸なら減少であり、すなわち平坦に戻そうという傾向のある現象なのである(たとえば水面・温度分布・濃度分布などにこういう傾向がある)。
 という新しい漢字を作って、読み方は「つと」にすべきだ、と前々から主張しているが、誰も聞いてくれない(;_;)。
という新しい漢字を作って、読み方は「つと」にすべきだ、と前々から主張しているが、誰も聞いてくれない(;_;)。