受講者の感想・コメント
青字は受講者からの声、赤字は前野よりの返答です。
対数の意味$a=\mathrm e^{\log a}$の使い方がわかってきた。logを取る。$\log(fg)=\log f+\log g$
今後使いこなしていきましょう。
指数、対数をやっていて、改めて意味や計算の仕方が実感できました。
どっちもこれからお世話になるものです。
指数・対数関数の微分についてやった。もともと微分の公式として覚えたものを実際にといてみるということはおもしろいなと思った。
公式みたいなのも、出し方は1通りでなく、いろいろあるもんです。
$\mathrm e^x$が$1+x+x^2/2+\cdots$ってなっているのは「お〜!!(・□・)」と思った!
昨日遅れて自動車税払ったんですけど延滞金なくてちょっと嬉しかったです(よかったー!)。あと、最近麺類を食べるようになりました。おいしいラーメン屋さんないかなー。
指数関数はいろんな方向から見つけることができるのが面白いところです。
私は疲れた時には天下一品のこってりラーメン食べに行きます。
${\mathrm d\over \mathrm dx}(\mathrm e^x)$や${\mathrm d\over \mathrm dx}(\mathrm e^{kx})$、${\mathrm d\over \mathrm dx}(a^x)$は違う式に見えて、関連していることがわかった。
そこを繋げて理解していきましょう
logはちょっと敬遠してましたが、試してみたら対数で微分するのは本当に簡単で驚きました。
敬遠しちゃだめですよ。仲良くなるととても有難い奴です。
指数関数の微分のときに、高校のときに習った公式がたくさん出てきたが、すっかり忘れているものもあった。「関連付けて覚える」ことはとても大事だなと思ったので、復習しながら挑戦してみたいと思う。
知識や概念は自分の頭に整理して置いておいてこそ、役に立ちます。
今日は指数関数対数関数の微分の話をして、いろいろな方向から微分を考えました。高校の教科書に並んでいた公式の導き方がわかったのでよかったです。
導ける式は「どこからきたか」も含めて理解しましょう。
今回は公式しか知らなかった指数・対数について詳しく知れてよかった。また、二階微分のことも知れたのでよかった。
中身をじっくり理解していきましょう。
微分の時、logを有効に使うと計算が楽になることがわかった。
logは使い途がいろいろあります。
対数微分で$y=x^x$の計算が今までどのような理屈で答を出せばよいかいまいちわからなかったけど、今日でわかった。
これから使っていってください。
${\mathrm d\over \mathrm dx}(f(x)g(x)),{\mathrm d\over \mathrm dx}\left({f(x)\over g(x)}\right)$の公式の求め方がlogを使って求められたこと、$\log a^b=b\log a$の仕組みを知っておもしろかったです。トイレに行きたかったのですが、今日の授業は聞きたい話が多かったので行けなかったです。
おもしろがってくれたのはいいけど、健康のためにもトイレは行っときましょう。
対数の微分や指数の微分が実はそんなに難しくなくて嬉しかった。
計算自体は単純ですね。
対数をもっと復習する必要があると思った。二回微分だと思ってた。
対数はこれからもずっと使いますよ。
eの値の求め方を初めて知った。微分しても変わらない関数の考え方に納得したし、eの値を忘れないと思う。忘れても求められる。
一度電卓叩いてみてください。
eの定義を思い出せてよかった。
微分の定義も慣れてきた。
このまま使いこなしていきましょう。
指数関数、対数関数の微分についてよくわかった。しっかり復習して身につけたい。
がんばりましょう。
指数関数・対数関数の微分の理屈がよくわかった。
n階微分の「かい」が「階」と書くことを初めて知った。
実はそうなんです。
一つの式の微分でもやり方はいろいろあってまだ知らないやり方が多くあるのだと気づきました。まだまだ自分でも見つけようと思います。
自分で探すのも楽しいですね。
$(f(x)g(x))'$をlogを使っておなじみの定理が出せるのがおもしろかったです。あと二階微分の意味がよくわかりました!!
一つの式にも色んな意味がある、ということを知っていきましょう。
f(x)のf'(x)をf(x)と同じ形にしたい→f'(x)のf''(x)をf'(x)の形と同じにしたい→以下同様→テーラー展開になる。よく理解できました。
テーラー展開の仕組みについてはまたじっくりやりましょう。
指数関数・対数関数の微分や二階微分について理解できた。
じっくり理解しておいてください。
対数の微分がよくわかった。対数の微分を分数関数の微分にしたりするのははじめて見てすごいと思った。
いろんな微分の方法を試してみてください。
$\mathrm e^x$の微分とか、どんどん増えていくところが興味深かった。
面白い関数です、指数関数。
logを使った微分のやり方がわかってよかったです。また図を使って理解を深めたいと思います!!
いろいろ自分でも図を描いてみてください。
三階微分、四階微分を調べるとよいことってあるんですか? 二階微分までで十分な気がしました。
状況によっては必要です。単にグラフ描いたりする程度なら二階まででいいかもしれません。
1階微分、2階微分は基礎ゼミでもやったので、間違えないと思う。
それはよかった。
高校までは公式を導くことの証明はしましたが、二階微分の極限を用いてその意味を理解することなく、ただ下に凸か上に凸か反射的にやっていたので新鮮でした。
そこはやはり意味がわかってこそ面白いですよ。
二階微分という漢字、間違えないよう注意します。
覚えておきましょう。
二階微分の理解が深まり、その重要性がわかった。
はい、これから先で重要です。
二階微分の階の漢字を初めて階と知った。回だと思ってた。微分終わるまえに理解しておきたい。
結構多いです、そういう人。
二階微分が$2\lim_{\Delta x\to0}{{f(x+2\Delta x)+f(x)\over2}-f(x+\Delta x)\over (\Delta x)^2}$で表せて、式の意味がわかったときは、そういうことなんだと思った。できれば三階微分の意味も教えて欲しいです。
一度作ってみるといいですよ。ただ三階から先は直観的にはわかりにくいです。
二階微分は凸か凹かを見る!!面白い!と思いました。三階微分の意味など、どれくらいまで何階まで意味があるのでしょうか?
三階以上になるとぱっと見てわからなくなってくるのです。
今日二階微分や一階微分について図やグラフを書くことで理解がしやすくなった。
図とグラフを書くことは大事ですね。
高校時代カッコつけてダッシュをプライムと読んでました。微積の授業で先生が二回微分と書いていた気がします(大学の)。
あれ??うっかりしたのかな>二回
だんだん難しくなってきたので質問しようかと思いましたが、よく考えると自分で納得できることが多いので、どうしても分からなかった時はしようと思います。
納得出来ないな、と思ったら質問よろしく。
タブレットのない前野先生の授業もおもしろかったです。自分も今後
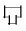
(つと)を使っていきたいと思います。
「そんな漢字ないぞ!」と言われないように気をつけて使ってください。
微積はとても頭が痛い。頑張る。
わからないところは質問どうぞ。
微分とても難しいです。しかも、センターの範囲の公式さえ忘れているという状況にあせりました。出なおしてきます。
公式は覚える必要はないですが、「なんでこういう式が出てくるか」という理屈のところを一度は理解しておくようにしましょう。
今日は当てられて答えましたが、左辺と右辺がヒントで教えてくれたシキと逆になっているのに気が付かなかったです。しっかり見直したいと思います。
じっくり考えてみておいてください。
忘れていたことがあったので復習になりました。
今度は忘れないように。
そろそろ難しくなってきそうな感じがしました。テストはあるのですか?
テストはあるにきまっているでしょう。期末テストやります。
授業がわかりやすいので微分の理解がしやすいです。
それはうれしいことです。
今回だいぶ前に授業でやったことが少しでてきたが、忘れている部分があったので、みなおしをもう一度します。
前にやったけど忘れている、というのは勉強の仕方が悪いからです。しっかり身につく勉強をしましょう。
後半、気がついたらねてしまった。次回からちゃんと集中して頑張ります。
あ〜、今日は結構寝ている人いたなぁ(T_T)。
これまで、なんとなく使っていた公式の成り立ちを知り、理解を深めることができました。
数学で「なんとなく使う」はやっぱり駄目です。
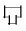 (つと)を使っていきたいと思います。
(つと)を使っていきたいと思います。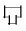 (つと)を使っていきたいと思います。
(つと)を使っていきたいと思います。