東京図書「よくわかる解析力学」サポートページ

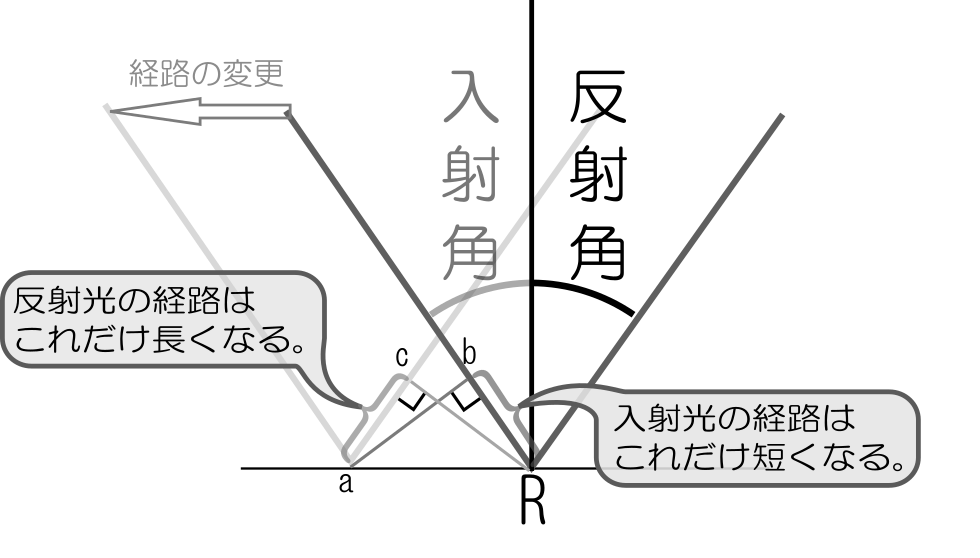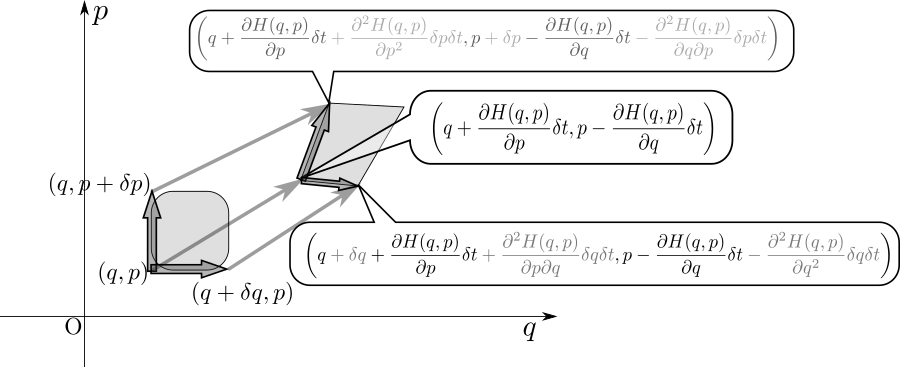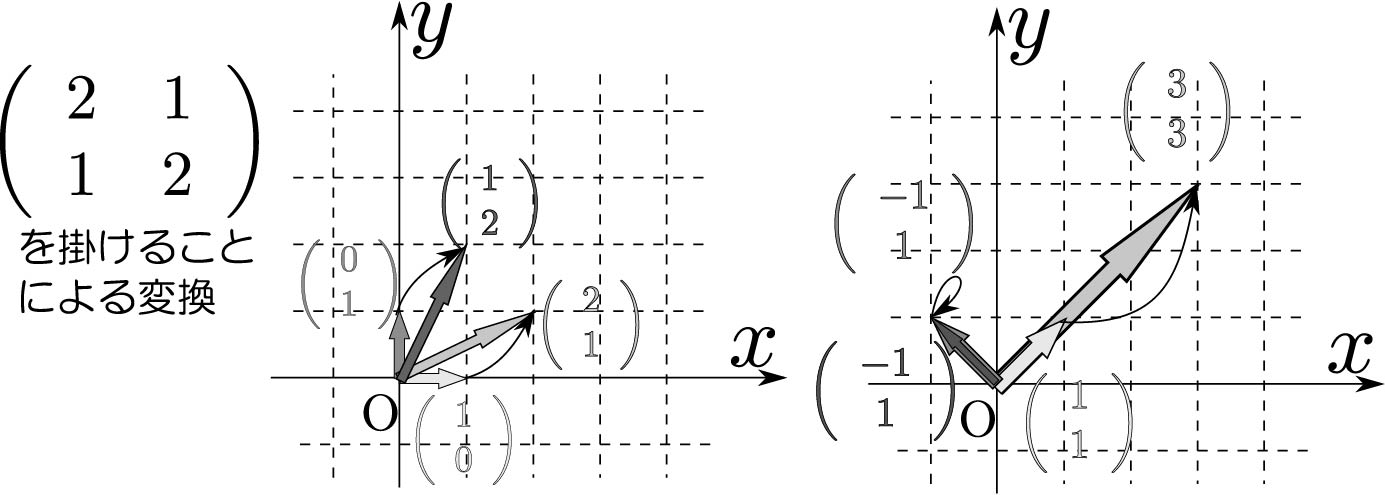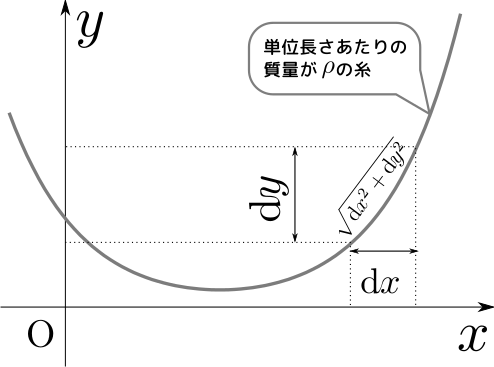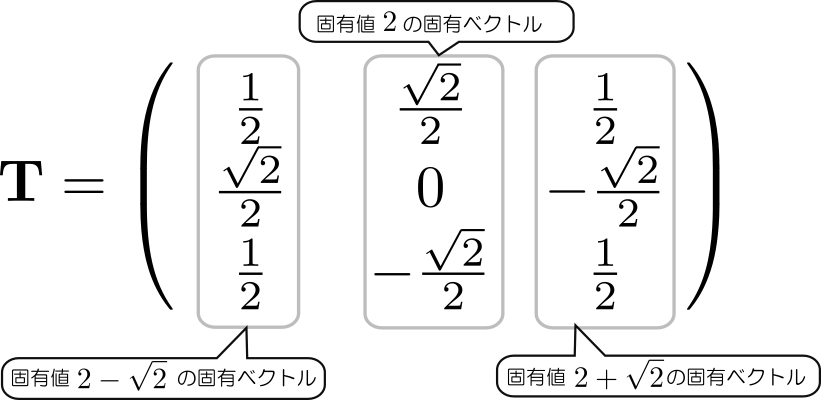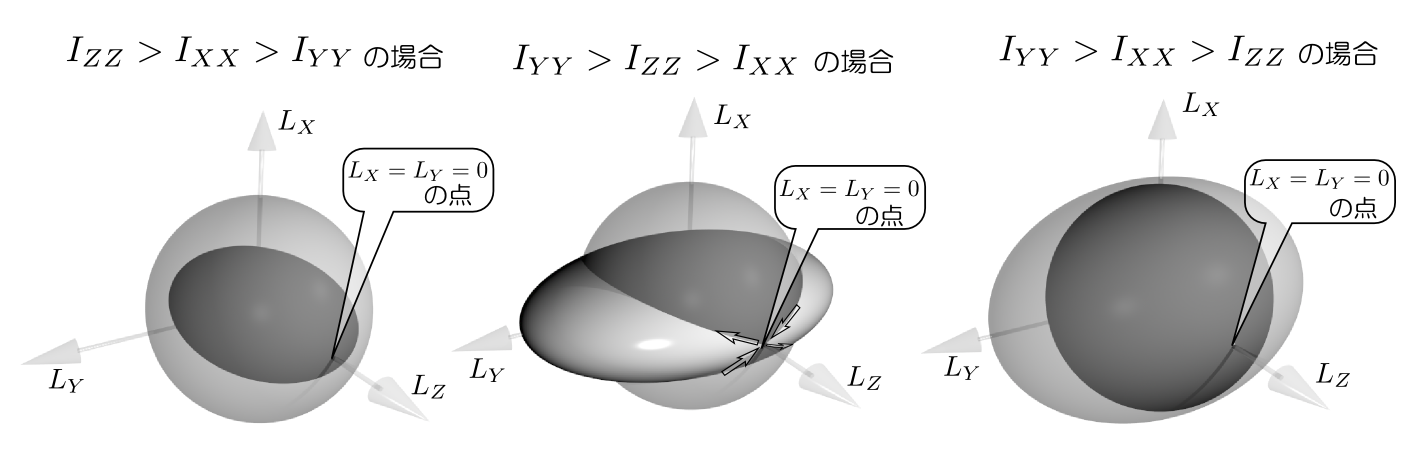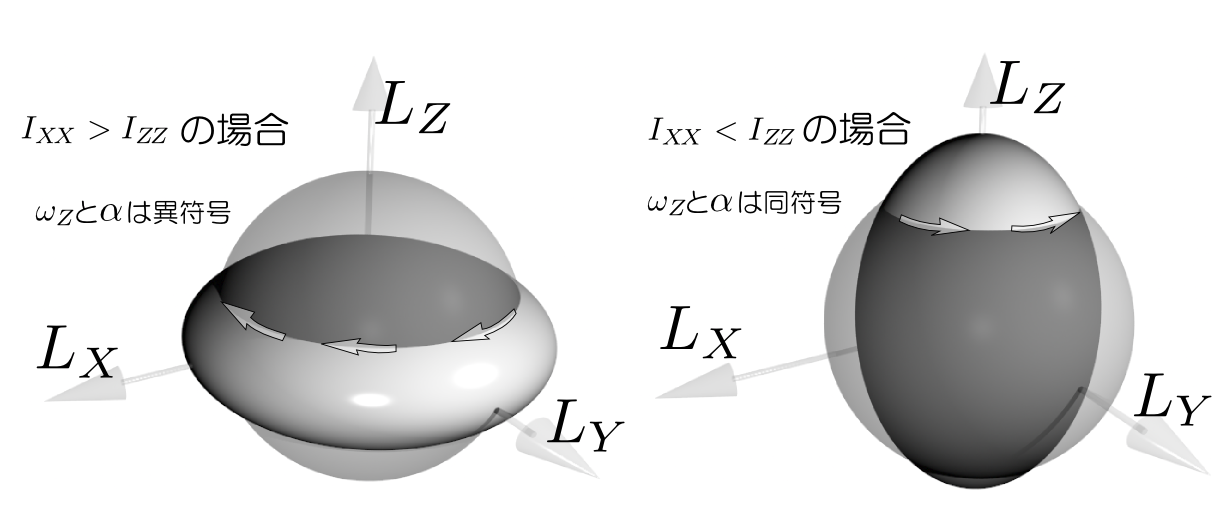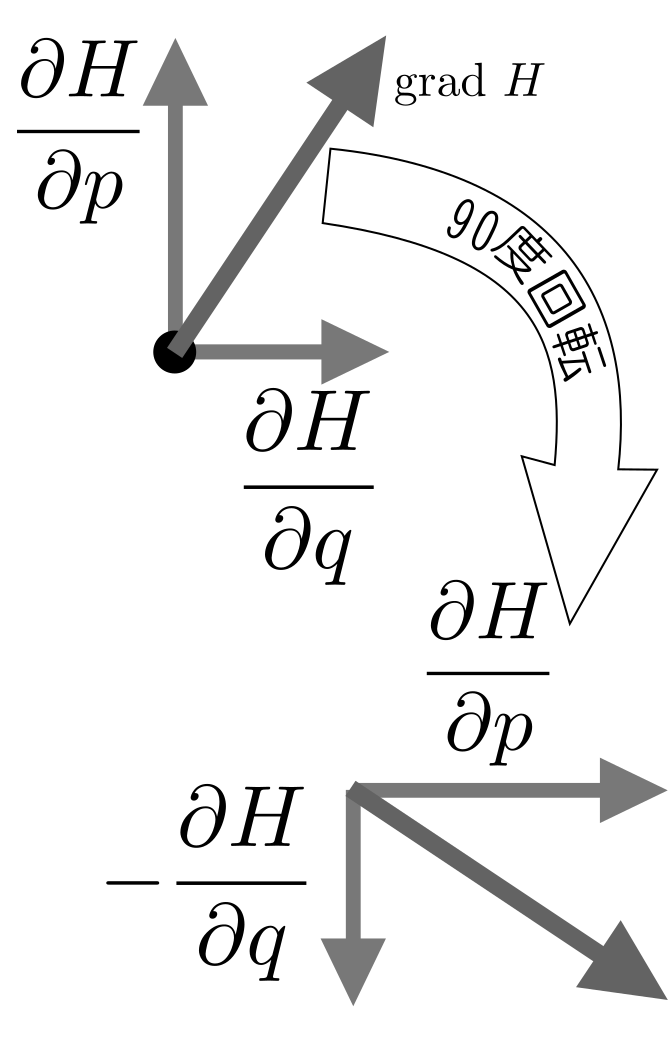
　このページは、「よくわかる解析力学」（前野昌弘著／東京図書）のサポートページです。

　出版社（東京図書）による新刊紹介のページはこちら。

　不明な点がありましたら、maeno@sci.u-ryukyu.ac.jpにメールするか、またはサポート掲示板に書き込んでください（サポート掲示板に書き込むとメールが届くようになっています）。

・「はじめに」より

・演習問題のヒントと解答

　ページ数が多すぎたため、章末演習問題のヒントと解答はPDFにて配布することにしています。ここからダウンロードできます。

・シミュレーションのページ

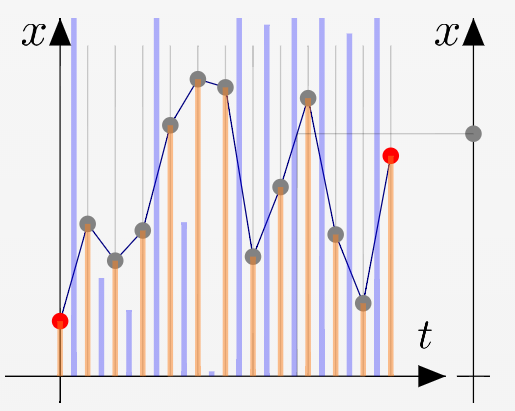
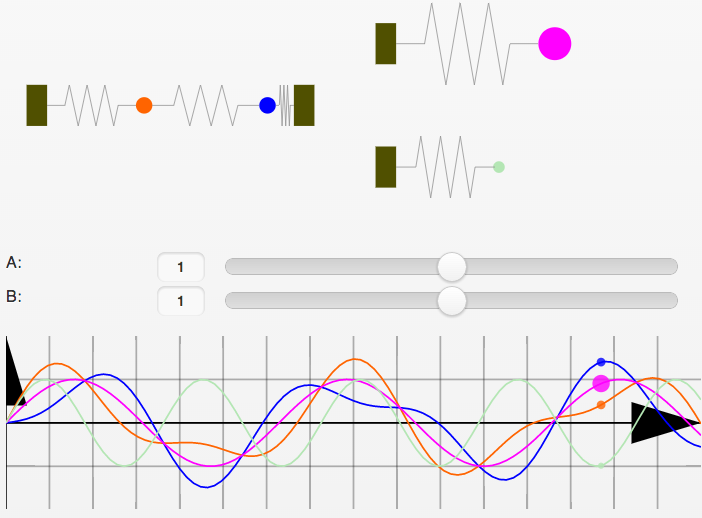
解析力学を理解するのに役立ついくつかのプログラムをこのページで公開しています。

・サポート掲示板

　wikiです。気がついたこと、感想などお寄せ下されば。

・ネット書店の売り場へのリンク

★のついているネット書店には、ユーザーによるレビューがあります。

• amazon★
• e-hon
• 紀伊國屋書店
• 楽天ブックス

・書評などへのリンク

• とね日記
• booklogの本書のページ
• 読書メーターの本書のページ

・店頭用ポップ

　以下のようなものを作成しました。クリックするとPDFがダウンロードできるので、書店の方よろしかったら使ってください。

・出版後に発見された内容のミスについて

　以下に、発見されたミスを記載していきたいと思います。

　これらの訂正部分のうち、数式・図版などを実際の本とほぼ同サイズになるように印刷できるPDFファイルがこちらです（ただし、簡単な文字の訂正などは含まれていません）。こちらをダウンロードして切り貼りしてくださってもよいです。

以下の間違いは第11刷で訂正されました。

• p29の「2.2.1 反射の法則」の1行目の「フェルマーの定理」は「フェルマーの原理」に修正。
• p164の(6.88)の$\displaystyle\sum_{i=1}^{N-1}$を$\displaystyle\sum_{i=0}^N$に訂正し、その後の「となる」の後ろに「（$y_0=y_{N+1}=0$）」を追加。さらに(6.89)の$\displaystyle\sum_{i=1}^{N}$も$\displaystyle\sum_{i=0}^N$に訂正。
• p364の(D.105)の次の${\partial P\over \partial p}\biggr|_{q,t}={\partial q\over \partial Q}\biggr|_{P,t}$の後ろに、「（(10.6)で、正準変換なので$J=1$とした式）」を追加。(10.6)の下に「→p245」をつける。
• p369の(D.131)の左辺にある$\delta_{k\ell m}$は$\epsilon_{k\ell m}$に訂正。

以下の間違いは第10刷で訂正されました。

以下の間違いは第9刷で訂正されました。

• p72の(3.48)の上「直交座標で」の前に「$k,K$を正の定数として」を追加。
• p108の(4.76)の$m$を$m_1$に、(4.77)の$m$を$m_2$に訂正。
• p148の冒頭「前節での作用」を「前節でのラグランジアン」に、(6.31)のすぐ上の「まず作用」を「まずラグランジアン」に訂正。
• p152の(6.53)の次の行の「2次以上を無視した作用」を「3次以上を無視したラグランジアン」に訂正。

以下の間違いは第8刷で訂正されました。

$\def\allc#1{\haiiro{\{\!\kuro{#1} \!\}}}$
• piiiの下から7行目の「考えて込んで」は「考え込んで」に訂正。
• pivの枠の中の10行目の「どういう学問を知りたい」は「どういう学問かを知りたい」に訂正。
• p15の下の方の「角度座標は」の「は」は削除。
• p16の補足の１行目「ineratial」を「inertial」に訂正。
• p38の(2.41)の次の行の文中の式は$\delta y(x_0)=\delta y(x_1)=0$に訂正。
• p61の(3.22)の上の行についている「→p336の(C.12)」を「→p336の(C.9)」に訂正。
• p65の3.3の６行目の「梯子の全質量」を$M$ではなく$m$に訂正。
• p66の問い3-2の図中の「ネジの頭は半径」の後を$r$から$R$に訂正。
• p70の図の中でVという文字が登場していますが、文字をUになおしてください。
• p71の脚注†19の冒頭、「$x$で微分して$ay$が出るために」を「$x$で微分して$-ay$が出るために」と訂正。最後の行の$F_y=ay$を$F_y=ax$と訂正。
• p92の(4.16)の最後の積分を$\int_{t_i}^{t_f}$に（積分の上端と下端をつける）。
• p110の(4.84)の下の「ラグラジアン」を「ラグランジアン」に訂正。
• p113の (5.6)の2行上の行の「式でててくる」を「式で出てくる」に訂正。
• p119の(5.30)を $$ {\partial L(r,\dot r,\dot\theta)\over \partial r}\biggr|_{\dot r,\dot\theta}-{\mathrm d\over \mathrm dt}\left({\partial L(r,\dot r,\dot\theta)\over \partial \dot r}\biggr|_{r,\dot\theta}\right)=0 $$ と訂正（括弧の位置）。(5.32)も同様に $$ {\partial \tilde L(r,\dot r,h)\over \partial r}\biggr|_{\dot r,h}-{\mathrm d\over \mathrm dt}\left({\partial \tilde L(r,\dot r,h)\over \partial \dot r}\biggr|_{r,h}\right)=0 $$ と修正。
• p130の２行目「、物体」を「物体、」に訂正。その後の「自由に動ける）物体」のあとに」（括弧閉じる）を挿入。
• p136の(5.96)の左辺第２項の偏微分で固定する変数を$\allc{q_\ast},\allc{Q_{\overline k}}$に変更。
• p137の問い5-4の１行目、$Y=X\tan \theta$を$Y=-X\tan \theta$に訂正。
• p140の９行目の「呼ばれる」のあとの）（括弧閉じる）を削除。
• p143の下の図を以下のように修正（「数字は、」の後の式）
  
• p154の6.3.1節の冒頭「三体連成振動（」を削除。
• p155の５行目からを、「$\left(\begin{array}{c}x_1\\ x_2\\ x_3 \end{array}\right)={\bf T}\left(\begin{array}{c}X_1\\ X_2\\ X_3\end{array}\right)$となるように新しい変数を導入して」と訂正してください。
• p159の(6.73)の上の行の「両辺を」と、(6.74)の下の行の「右辺の」を削除。(6.75)の下の行の$2\mathrm i\sin{\alpha\over2}$は$-2\mathrm i\sin{\alpha\over2}$に修正。
• p161の下から２行目の「ぐるりと回るベクトルを一周」を「ぐるぐる回るベクトルを$2p$周」に修正。
• p162の6.4の4行目の「グランジアン」を「ラグランジアン」に訂正。
• p177の(7.24)の$\omega\times\vec X$を$\vec\omega\times\vec X$に訂正。
• p184の7.2.5のタイトル「特定の軸に」を「特定の軸の」に訂正。
• p190の演習問題7-4の1行目の「細い円板」は「薄い円盤」に訂正。
• p205の下から４行目の「オイラー・ラグランジュ・ラグランジュ」は「オイラー・ラグランジュ」に訂正。
• p206の9.1.2の１行目の「ラグラジアン」を「ラグランジアン」に訂正。
• p212の(9.31)の次の行中の$\dot q_i(t)=v(t)$は$\dot q_i(t)=v_i(t)$に訂正。
• p218の２行目の「$y$軸」は「$q$軸」と訂正。
• p230の(9.74)の１行目 $$ \sum_{i,j}\left(\biggl({\partial A\over \partial q_i}{\partial^2 B\over \partial q_j\partial p_i}-{\partial A\over \partial p_i}{\partial^2 B\over \partial q_j\partial q_i}\biggr){\partial C\over \partial p_j}-\biggl({\partial A\over \partial q_i}{\partial B\over\partial p_j \partial p_i}-{\partial A\over \partial p_i}{\partial^2 B\over \partial p_j\partial q_i}\biggr){\partial C\over \partial q_j}\right) $$ を $$ \sum_{i,j}\left(\biggl({\partial A\over \partial q_i}{\partial^2 B\over \partial q_j\partial p_i}-{\partial A\over \partial p_i}{\partial^2 B\over \partial q_j\partial q_i}\biggr){\partial C\over \partial p_j}-\biggl({\partial A\over \partial q_i}{\partial^2 B\over\partial p_j \partial p_i}-{\partial A\over \partial p_i}{\partial^2 B\over \partial p_j\partial q_i}\biggr){\partial C\over \partial q_j}\right) $$ に訂正（$B$の前の$\partial$を$\partial^2$に）。その次の(9.75)を $$ \displaystyle \begin{array}{rl} &\sum_j\left({\partial^2 B\over \partial q_j\partial p_i}{\partial C\over \partial p_j}-{\partial^2 B\over\partial p_j \partial p_i}{\partial C\over \partial q_j} - {\partial^2 C\over \partial q_j\partial p_i}{\partial B\over \partial p_j} +{\partial^2 C\over\partial p_j \partial p_i}{\partial B\over \partial q_j}\right) \\[3mm] =&{\partial\over \partial p_i}\sum_j\left( {\partial B\over \partial q_j}{\partial C\over \partial p_j}-{\partial B\over\partial p_j }{\partial C\over \partial q_j} \right) ={\partial\over \partial p_i}\PB{B,C} \end{array} $$ に訂正（$\sum_j$を追加）。
• p238の(9.96)の次の行の「オイラーの運動方程式」の下についている文字を「→p181の(7.40)」に訂正。
• p239の脚注†34の$\dot\psi,\dot\phi,\dot\psi$を$\dot\psi,\dot\theta,\dot\phi$に修正。
• p242の演習問題9-4の「対称ゴマ」を「対称コマ」に訂正（用語の統一）。
• p252の４行目の「単振動の解と一致している」のあとに（上の二つの式の$A,\alpha$は前ページの$A,\alpha$とは別）と追加。
• p263の脚注†24の「凸関数でない」の下の文字を「→p333」に訂正。
• p275脚注†36の「からもしれない」を「かもしれない」に訂正。
• p278の練習問題10-3の問題文中の$\delta$を$\epsilon$に訂正。
• p283の図中の$t_1-t_0$は$t-t_0$に訂正。図の下の「$p_i$が3つ」を「$\alpha_i$が3つ」に訂正。その３行下の「パラメター」を「パラメータ」に訂正。脚注６の$\vec x_1=\vec x_0$は$x_i=x_i^{(0)}$に訂正。
• p284の１行目の$\vec x_0$を$\vec x^{(0)}$に訂正。
• p287の脚注†12の式を、$\int\sqrt{1-{x^2\over A^2}}\mathrm dx={x\sqrt{1-{x^2\over A^2}}\over 2}+{A\over 2}\arcsin {x\over {A}}+C$に訂正。
• p290の図の中の式を$W(x,y)=\sqrt{2mE_x}x -{2\sqrt{2m}\over 3mg}\left(E_y-mgy\right)^{3\over 2}$に修正（第２項の符号）。p290の5行目の「ともに$+$」を「順に$+,-$」に修正。その５行下の「(11.40)にある複号が$+$」を「(11.40)の二つめの複号が$-$」に訂正。その次の行の「2番目の複号$+$」と「2番目の複号$-$」を交換。
• p295の下の方、「$r$と$\epsilon$は楕円の形を示すパラメータ」は「$r_0$と$\epsilon$は楕円の形を示すパラメータ」と訂正。
• p298の第１２章のタイトルの「さいごに」→「おわりに」に訂正。
• p306の下から２行目の「用意に」を「容易に」に訂正。
• p310の(A.27)の上の行の$(a^{-1})_{ji}$を$(a^{-1})_{ij}$に訂正。
• p319の(B.5)の２行上の「二階微分微分可能」は「二階微分可能」に訂正。同ページの(B.6)の２行上の「表現すれば書けば」は「表現すれば」に訂正。
• p330のB.5.1の前の行の(Legendre transfomation)を(Legendre transformation)に訂正。
• p332の(B.60)の2行上の「$y$を微分」を「$y$で微分」に訂正。
• p346の問い2-1のヒントの１行目の「横の高さ」を「横幅」に修正。
• p349の問い10-4のヒントの、「(10.56)の両辺を$p$を一定として$q$で微分したもの」を「(10.56)の両辺を$q$を一定として$p$で微分したもの」に訂正。
• p350の(D.16)を $$ p_x = m\dot x= m{\mathrm d \over dt}(r\cos \theta)= m\dot r \cos \theta - mr\dot\theta \sin \theta=p_r \cos \theta -p_\theta {\sin \theta\over r} $$ と修正。
• p351の問い11-1のヒントの中の$x^{(1)}_i,x^{(1)}_j$と$t_1$を、それぞれ$x_i,x_j$と$t$に訂正。
• p357の問い5-2の解答内の$U$をすべて$V$に。
• p360の(D.80)の行頭の$=$二つのあとに$2$を挿入。
• p360の(D.81)を $$ -mg\epsilon(t_f-t_i)=\epsilon\biggr(m\dot{z}\bigr|_{t_f}-m\dot{z}\bigr|_{t_i}\biggr) $$ と訂正。その上の「書いたように、、」の読点を一つ削除。
• p363の問い10-5のヒントの２行目の「同様に$p=p(Q,P(Q,P))$」を「同様に$p=p(q,Q(q,p))$」と訂正。
• p364の(D.102)の下の「独立であるとした」は「独立であるとして」と修正。
• p366の脚注†1内の「右上の${\partial x\over \partial p_x}$」と「左下の${\partial p_x\over \partial x}$」はそれぞれ、「右上の${\partial x\over \partial p_r}$」と「左下の${\partial p_x\over \partial r}$」に訂正。
• p368の1行目「$p_y-{qB\over 2}x$が定数である。」を「$p_y+{qB\over 2}x$が定数である。」と訂正。
• p368の(D.125)の右側の最後の行は $$ =\left(\!\begin{array}{c}aex+afy+bgx+bhy\\cex+cfy+dgx+dhy\end{array}\!\right) $$ に修正。
• p369の(D.129)の２行上の「$P\neq\ell$の時の答は0である」を「$p\neq\ell$の時の答は0である」に訂正。

以下の間違いは第7刷で訂正されました。

• p30の真ん中の図を
  
  に変更。これに伴い、図の下にある「$\overline{\rm bR}$の分だけ入射光の経路は縮む」を「$\overline{\rm aR}\sin$(入射角)の分だけ入射光の経路は縮む」に、「反射光の経路は$\overline{\rm ab}$」を「反射光の経路は$\overline{\rm aR}\sin$(反射角)だけ伸びる」に訂正。その次に文中にある式$\overline{ab}=\overline{bR}$は$\overline{ac}=\overline{bR}$に訂正。
• p118の冒頭、「${\partial L\over\partial y}$から」を「${\partial L\over\partial y}=0$から」に訂正。
• p186の脚注の文章を以下のように変更。「(7.62)を微分して、それぞれの${\mathrm d\omega_i\over\mathrm dt}$を、(7.39)から(7.41)を使って書き直すとエネルギー保存がわかる。」
• p202の(8.36)の次の行についている「→p336の(C.12)」「→p336の(C.9)」に訂正。
• p214の(9.40)の最後の行を $$ \int \biggl(\sum_i \left(\delta q_i \left(-\dot p_i -{\partial H\over \partial q_i}\right)+\delta p_i \left(\dot q_i-{\partial H\over \partial p_i}\right)+{\mathrm d(p_i\delta q_i) \over \mathrm dt}\right)\biggr) $$ に変更（${\partial H\over \partial p_i}$の後ろにあった２個の）のうち一つを${\mathrm d(p_i\delta q_i) \over \mathrm dt}$の後ろに移動）。
• p351の【問いC-1】のヒントの最後、$\sum_{\ell,m}C_\ell D_m$の部分を$\sum_{\ell,m}\epsilon_{i\ell m}C_\ell D_m$に訂正。
• p369の【問いC-1】の解答の最後に、以下を追加。
  (C.13)の方は、ヒントより、$(\vec A\times\vec B)\cdot (\vec C\times \vec D)=\sum_i \sum_{j,k}\epsilon_{ijk}A_jB_k\sum_{\ell,m}\epsilon_{i\ell m}C_\ell D_m$に$\sum_{i} \epsilon_{ijk}\epsilon_{i\ell m}=\delta_{j\ell}\delta_{km}-\delta_{jm}\delta_{k\ell}$を代入して、 $$ \sum_{j,k,\ell,m}\left( \delta_{j\ell}A_j C_\ell\delta_{km}B_k D_m-\delta_{jm}A_j D_m\delta_{k\ell}B_k C_\ell\right)=(\vec A\cdot\vec C)(\vec B\cdot\vec D)-(\vec A\cdot\vec D)(\vec B\cdot\vec C) $$ となる。

書籍サポートページの目次に戻る