Processing math: 80%

自然科学のための数学2014年度第６講

　今日は微分の定義のお話の続きから。

極限としての接線の傾き

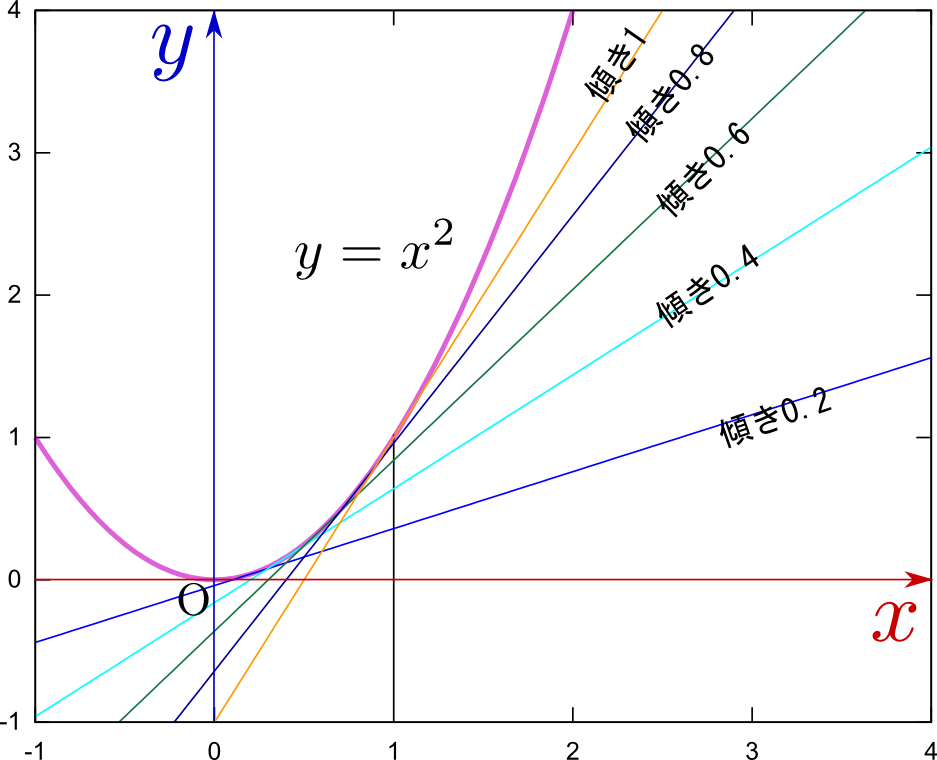
　 ${y}=f(x)=x^2$ という、単純な関数の場合で傾きの計算をしてみよう（傾きの変化の様子を次のグラフに示した）。

　この場合、独立変数と従属変数であるxと ${y}$ は ${y}=x^2$ という関係式を満たしながら変化するのだから、変化後も

$\begin{equation} \underbrace{{y+\Delta y}}_{変化後の{y}}=(\underbrace{{x+\Delta x}}_{変化後のx})^2 \end{equation}$

という式が成立する。この式の右辺を $({{x+\Delta x}})^2=x^2 + 2{x\Delta x} + ({\Delta x})^2$ と展開した後、元の式 ${y}=x^2$ と辺々の引き算を行なう。

$\begin{equation} \begin{array}{rrrll} & {y}&+{\Delta y}=&x^2+&2{x\Delta x}+({\Delta x})^2 \\ -)& {y}&=&x^2 &\\ \hline &&{\Delta y} =&& 2{x\Delta x}+ ({\Delta x})^2 \end{array}\label{dy2xdx} \end{equation}$

　こうして二つの変数の変化量の間は、 ${\Delta y}=2{x\Delta x}+({\Delta x})^2$ という関係があることがわかった。当たり前だが、 ${\Delta x}=0$ と置くと、 ${\Delta y}=0$ になる。

　ここで、

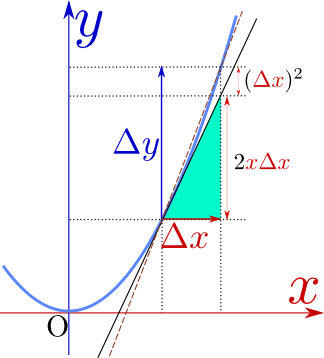
$\begin{equation} {{\Delta y}\over {\Delta x}}=2x+{\Delta x} \end{equation}$

となるが、この量は右の図に破線で描いた直線の傾きになる。

　右のグラフに $2{x\Delta x}$ と $({\Delta x})^2$ を描き込んだ。これを見ると $2{x\Delta x}$ は ${\Delta y}$ のうち主要な部分を占めていて、 $({\Delta x})^2$ の方は「ちょっとした修正」程度に付け足された量だという印象を受ける（図でも確認しよう）。

　試しに ${\Delta x}=0.01$ としてみると、 $\left({\Delta x}\right)^2=0.0001$ になる。つまりΔxをどんどん小さくするという文脈において、 $\left({\Delta x}\right)^2$ は「Δxより、もっと小さい」量になっている。

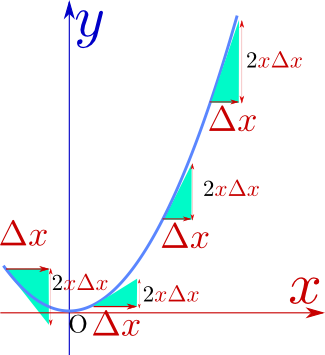
　 ${\Delta x}\to0$ という極限を取っていくと（この時同時に ${\Delta y}$ も0に近づくわけだが）、第２項はなくなってしまって、

$\begin{equation} \lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}}=2x\label{diffxsq} \end{equation}$

がわかる。つまり接線の傾きは $2x$ である。xが変化すると傾き ${{\Delta y}\over {\Delta x}}$ が変化する様子を示したのが右のグラフである。各々の場所において接線の傾きが変化しつづけている。 $x<0$ では傾きも負になっていることに注意しようx=0のところでは傾き0、すなわち水平な線が接線となる。しかし、図では高さ0の三角形になって見えなくなってしまうので描いていない。}。

　Δxが小さい場合に2xの部分が重要であるということを確認するために、x=1として、Δxを変化させていった時の各項の様子を表にしてみると、

Δx	x+Δx	(x+Δx)²	2xΔx	(Δx)²	2x+Δx
1	2	4	2	1	3
0.1	1.1	1.21	0.2	0.01	2.1
0.01	1.01	1.0201	0.02	0.0001	2.01
0.001	1.001	1.002001	0.002	0.000001	2.001
0.0001	1.0001	1.00020001	0.0002	0.00000001	2.0001

のようになる。Δxを小さくするに従って、 ${{\Delta y}\over {\Delta x}}$ は2（2xの、x=1のときの値）に近づく。つまり、「Δxが0に近づいた時の値」が2である。

では次のページで、動く図で「極限」を取っている様子を見よう。

自然科学のための数学2014年度第６講

極限としての接線の傾き

目次