「よくわかる電磁気学」(東京図書)サポート掲示板(2018年1月30日まで) †
オームの法則について †
ss? (2018-01-25 (木) 16:30:03)
電気回路では導線を抵抗0としますが、V=RIで0=0×Iで電流は任意(外部により決まる)と考えられますが、オームの法則J=σEを用いた場合には
J=∞×0(E=-gradV=0)により電流は不定形なので任意と考えてもよいのでしょうか。
あるいは、現実には抵抗があるため、導線にも電位差が生じ、電流が流れるのだと考えるのが正しいのでしょうか。
とはいえ、p.169では導線の電位を一定としているため、導線の抵抗は0としているのではないかと思うのですが(抵抗≠0だと電位一定→E=-gradV=0→J=σE=0となるため)、何か勘違いをしているのでしょうか。
- 「抵抗0の導体」の存在を仮定するなら、そこに流れる電流は外部の条件で決まる、と考えるのが物理的に正しいです。 -- 前野?
- p169では導線の抵抗は0として考えてます。 -- 前野?
P.269 †
鮒27? (2018-01-19 (金) 20:15:41)
11.5の5行上 B=rotA でAにベクトル記号が抜けています。
- 御指摘ありがとうございます。次の刷で訂正します。 -- 前野?
演習問題4-2 †
鮒27? (2018-01-18 (木) 22:54:15)
解答(E.45)で誘電率に関する式が書かれていますが
異方性の誘電体の場合にもこれは成立するのでしょうか?
- いえ、これは異方性でない場合の式です。 -- 前野?
- 分かりました。ありがとうございます。 -- 鮒27?
P.145 電束密度 †
鮒27? (2018-01-16 (火) 21:48:32)
電束密度が理解できていません。
特にDの定義で出てくるEは下の①~③の考えでよいのでしょうか?
①真空中
D=(ε_0)E : このEは真空中の電場
②誘電体中(4.17)
D=(ε_0)E + P : このEは誘電体中の電場 (上の①の電場より大きさが弱くなる)
③誘電体中(4.19)
D=εE : このEは誘電体中の電場(ただし上の②の電場とは大きさが異なる)
あと、真空中の一様な電場Eの空間に、ある適当な誘電体を置いた時、
上で示した①、②、③の式は等式で結んでいいのでしょうか?
「今度こそ納得する物理・数学入門」の疑問16も併せて読んでいるのですが
どうもよく分かりませんでした。
- それについては本に書いてある通りで、1も2も3も正しいです。ただし、3については誘電体が異方性のある奴(外から掛ける電場と分極Pの方向が一致しないような物質)については成立しません。 -- 前野?
- 1,2,3は等式で結んでいいかといえば、それぞれ適用範囲が違うのだから結べる場合もあれば結べない場合もあります。あたりまえですが、P=0ならば1と2は同じだし、PがEと同じ方向なら2と3は同じ式です。 -- 前野?
- 例えばP.149の例で誘電体が電荷Qを中心として球状に広がっているとします。誘電体の外側が真空の場合、誘電体中でも真空中でもD=Q/4πr^2となると思います。これは電束の向きと境界面が垂直なので、P≠0でも上で示した①=②が成り立っているのでしょうか? -- 鮒27?
- その例では、真空中でも誘電体中でもDは同じ式ですが、Eは異なります。よって①と②の片方しか成り立ちません。 -- 前野?
- なるほど確かにそうです。 ①~③の適用条件をごちゃ混ぜにしていたのと、(何故か)Dはいつも同じと思い込んでいたため色々と分からなくなっていましたが、先生の回答と演習問題4-2を再度解いてみて電束密度について整理できたと思います。 どうもありがとうございました。 -- 鮒27?
演習問題9-3 †
鮒27? (2018-01-13 (土) 18:34:27)
p7w (4)のヒント
微小量とj 考えて → 微小量と考えて
かと思います。
P.236 問題文の(4)で ”Δzは微小だとして” とありますが、これの扱いが分かりませんでした。(1)で求めたようにB⊥=rΔB/2Δz なので、Δzが微小ならΔBも微小だろう、というのは分かるのですが、これから(4)のヒントにあるΔv⊥,Δv||が微小であることにどのようにつなげればいいのでしょうか?
- タイプミス報告ありがとうございます。もう一つの件ですが、(1)の式を出した時点で、Δzが微小だということをもう使ってます(微小じゃなかったらもっと複雑な積分が必要です)。 -- 前野?
- Δzが微小という前提があってこそ(1)のB⊥が求まるし、(2)、(3)のΔvもB⊥を利用して求められる。 だから(4)で運動エネルギーの変化を求めるときも(1)~(3)の結果を使うために、前提である”Δzが微小”を記しているのですね。 ありがとうございました。 -- 鮒27?
演習問題9-2 †
鮒27? (2018-01-13 (土) 15:56:58)
解答(E.82)の振幅aですが、これは(E.81)でA=|A|e^iαとした結果、つまりa = |A|ということでしょうか?
- 未定の定数なので何と書いてもいいですが、関係は$a=|A|$です。 -- 前野?
- 分かりました。ありがとうございました。 -- 鮒27?
P.223 左下の図 †
鮒27? (2018-01-11 (木) 20:51:55)
電子の運動だと思いますが、射影した円の矢印が逆向きではありませんか?
- 確かに、これは射影を間違えてますね。次の版で訂正します。 -- 前野?
P.218 (9.8) †
鮒27? (2018-01-11 (木) 20:47:31)
∇ですが、添え字の2が必要ないでしょうか。
- この∇が微分している相手は$x_2$のみの関数なので、明示しなくても$x_2$の微分だとわかるだろう、ということで書いていません。 -- 前野?
- 分かりました。ありがとうございます。 -- 鮒27?
P.189 上から6行目 †
鮒27? (2018-01-09 (火) 20:52:32)
”図のような円形電流・・・”とあり、おそらく図の黒っぽい円を指していると思いますが、これは円形磁場ではないのでしょうか? 磁場をさかのぼっていくのでV=0,1,2・・・になると思ったのですが。
- 黒い丸は磁場です。電流は灰色の方です。 -- 前野?
- そういうことでしたか。ありがとうございました。 -- 鮒27?
P.207 (8.29) †
[[鮒27 ]] (2018-01-09 (火) 20:32:43)
左辺にベクトルの大きさを表す記号||は必要ないのでしょうか?
- すいません、Bにはベクトル記号がいりません。 -- 前野?
- 分かりました。ありがとうございます。 -- 鮒27?
P.197 (8.6) †
鮒27? (2018-01-05 (金) 14:05:09)
(8.6)を解く方法がどうしても分かりませんでした。
まずz'-z = rtanθとしていますが、このθは(8.6)の右の図でいうとどこになるのでしょうか。 また(8.6)の分母が(z-z')なのに z'-z = rtanθとしている理由も分かりませんでした。 (このようにおけば(8.6)から(8.7)が導き出せるのは分かりました。)
- 積分で分母に$(1+x^2)^n$のような形がでてきたときに、$x=\tan\theta$とおいて積分する、というのはよくある積分のテクニックなので、それを使っていると思っていただいてもいいです。ここでは分母に$r^2+(z-z')^2$があるので、$r^2(1+{(z-z')^2\over r^2})$と書き直すと考えて、${(z-z')^2\over r^2}$の部分が$x^2$だと思えば、$\tan\theta={z-z'\over r}$になりますね。 -- 前野?
- θの図形的意味については、底辺がrで高さが$z-z'$の直角三角形が図にあるので、それだと思えばいいでしょう。 -- 前野?
- z'-z=rtanθと置いた図形的な意味がやっと分かりました。 こうすると確かにー∞ → ∞ が ーπ/2 → π/2に対応しますね。 ありがとうございました。 しかし教えていただいた積分のテクニックを使った方が間違いなくできそうです。 -- 鮒27?
p132 演習問題3-7について †
ぶつりすと? (2018-01-04 (木) 23:44:17)
3.7.3を参考にして単位面積あたりの斥力を計算したのですが、答案ではそのあとなぜか体積要素をかけて計算処理をおこなっていました。全体を面積分するのだったら面積要素をかけるのではないのだろうかと疑問に思いました。あと体積要素として導かれた数式がなぜ答案のようになるのか理解が出来ませんでした。教えていただきたいです。
- ああすみません、これは「体積要素」と書いてあるのが間違いで「面積要素」です。 -- 前野?
P.124 下から5行目 †
鮒27? (2018-01-03 (水) 12:36:29)
”エネルギーはQVとなる。”とありますが、コンデンサーが蓄えるエネルギーがQVなのでしょうか?
P.171も読むと外部がする仕事がQVで、コンデンサが蓄えるエネルギーはあくまでも1/2*QVに思うのですが。
- 「V が外部から与えられた電位差であって電荷が移動しても変化することがないような関数なら、」QVになるという話です。コンデンサの場合はVは変化しますから、もちろんQBではありません。 -- 前野?
- なるほど、仮想的な場合にそうなるということですね。 どうもありがとうございました。 -- 鮒27?
p130 問3-3について †
としあけ? (2018-01-02 (火) 12:14:46)
p130問3-3の問題について、微小面積×単位面積当たりの張力の面積分で面全体に働く張力を求めるという問題なのですが、答えに載っていた微小面積の取り方に疑問があります。半径Ltanθ、Ltan(θ+dθ)の円の面積を用いてθを0からπ/2の範囲で面積分をしているようなのですが、円を使って面積分をしている理由がよくわかりません。円を使った場合たとえばθ=0の円はθ=π/2の円の円周内に入ってしまい計算がうまくいかない気がします
- ヒントに書いてある(B.6)の面積は円の面積ではなく『半径$L\tan(\theta+\mathrm d\theta)$の円の面積』と『半径$L\tan\theta$の円の面積』の差です(つまり円と円にはさまれた円環部分)。 -- 前野?
- 積分は円環ごとの寄与を足していくという計算になりますので、シータが違う部分は重なってしまうことはないです。 -- 前野?
- あー納得しました。ありがとございます -- としあけ?
章末問題11-1(3)について †
ねんまつ? (2017-12-31 (日) 17:08:27)
章末問題11-1(3)において磁束密度が時間的に変化する際の電場を求める際に、答えでは∮E・dx=∂φ/∂tを用いて計算をしていたのですが、V=-dφ/dtの関係から見ても∂φ/∂tにマイナスが付いていないことにとても違和感があります。どこかでマイナスが相殺されたような記述も見当たらないのですが、どういう計算しているのでしょうか?
- 符号の定義の仕方は258ページにある通りですが、ここでは実は強さ(絶対値)にしか興味がないので両辺が正になるように計算してます。 -- 前野?
- 力の大きさを求めているだけだったんですね。ありがとうございました。 -- ねんまつ?
P.121 (3.88) †
鮒27? (2017-12-29 (金) 00:45:46)
(3.88)以降で「自分自身の作る電位は勘定に入れない」説明があり、これは納得できるのですが、この理屈でいくと自分自身以外の電位も勘定できないことになりませんか? 自分自身以外の場合、分母は微小領域のサイズの3乗に比例し、分母は微小でないサイズとなり、極限をとると0になるように思います。 どのように考えればいいか教えていただけませんか?
- (3.88)の後に書いてあるのは「発散しない」説明です(点電荷で自分自身の電位による位置エネルギーを計算すると発散してしまう)。 -- 前野?
- 自分自身以外の作った電位に自分の電荷密度を掛けて積分する場合、電位は有限量、微小体積内の電荷量は無限小です。しかし微小体積を集めてきて(積分して)計算すれば0でない値が残ります。 -- 前野?
- 確かにそうです。積分することが考えから抜けていました。ありがとうございました。 -- 鮒27?
演習問題3-2 †
鮒27? (2017-12-27 (水) 23:26:54)
(a),(b),(d)の電位ですが、積分定数Cをつけてもよいのでしょうか?
( 例えば(b)なら V = -kxy + C )
- もちろんつけても構いません。 -- 前野?
- 分かりました。ありがとうございます。 -- 鮒27?
偏った電位が一様な電荷分布を与えるのが分かりません †
技術者? (2017-12-27 (水) 17:11:18)
改めて電磁気を勉強し直しているものです。良い教科書、ありがとうございます。
質問は、3.8 章末演習問題の【演習問題3-1】において、一様でない電位 $V = k x^2$ が
一様な電荷分布 $ \rho = - 2 k \epsilon_0 $ を与えることがしっくりきません。考えて見ると $ V = \frac{1}{3} k ( x^2 + y^2 + z^2 ) $ も同じ電荷分布を与えるので、こっちだとしっくりくるのですが…。
- しっくりこないと言われても、どちらもちゃんとしたMaxwell方程式の解なので、優劣などはないです。あえていうなら$x^2+y^2+z^2$の方が対称性がいい程度でしょう。 -- 前野?
- 微分方程式ですので、同じ電荷分布を与える解がたくさんあるのは普通のことです(境界条件があれば一つに決まりますが、ここではまだ与えていません)。 -- 前野?
- ご回答、ありがとうございました。一様な電荷分布ってどんな電場を生じるのか不思議でしたが、境界条件をつけた段階で系としては一様ではなくなるんだなと理解しました。 -- 技術者?
演習2-4について †
ぶつりすと? (2017-11-11 (土) 17:39:17)
演習問題2-4で直交座標における電場Eの分子を(x.y.z)=(ρx, ρy , 0)と置いていたのですが、z軸の単位長さあたり電荷量であるρにxやyをかけた場合の物理的意味がよくわかりません。解説お願いします。
- そりゃ、分子だけ見て物理的意味を考えたってわからないでしょう。問題文に書いてあるとおり、電場の大きさは${\rho\over2\pi \varepsilon_0 r}$で、その$x$成分を取り出すには${x\over r}$を掛ければよい、という計算の結果、分子が$\rho x$になったというだけのことです。 -- 前野?
- ありがとうございました -- ぶつりすと?
p38の電場の計算 †
でんき? (2017-11-04 (土) 09:50:49)
p38の電荷がσで分布している球面の電場を求める問題でθの積分範囲が0→πとなっていますが球面全体を積分するなら0→2πまでではないのですか?
- θの定義をよく見て下さい。極座標のθはθ=0で北極、θ=πで南極ですから、そこまでで終わりです。 -- 前野?
p.244 アルミニウムの磁気感受率 †
愛読者? (2017-10-26 (木) 00:04:08)
最新版で以下が訂正済みの節はお詫びしますが、
p.244 アルミニウムの磁気感受率は、2.1X10exp(-4)ではなく、
正しくは 2.1X10exp(-5)ではないでしょうか。
- すいません、だいぶ前に書いたので何を参考にしたのかすら覚えてないのですが、写し間違いのようです。御指摘ありがとうございます。 -- 前野?
- お忙しい中をご確認ありがとうございました。 -- 愛読者?
5章電流と回路 式の導出について †
蔵? (2017-10-08 (日) 18:58:10)
式5.4から式5.5への導出がいくら考えても出来ません。
どのような計算をすれば導けるでしょうか。
お手数ですがよろしくお願い致します。
- これが答えであることは続きで示してますが、(5.4)から(5.5)を直接導きたいということですね? でしたら${\mathrm dx\over\mathrm dt}=v$とまず置きます。 -- 前野?
- すると$m{\mathrm dv\over\mathrm dt}=eE-kv$となります。これはいわゆる定数係数の線形微分方程式なので、その手順どおりで解けます。 -- 前野?
- 手順通りでなく考えるならば、「ややこしい部分を定数にしてまとめてしまえ」ということで、$eE-kv=X$と右辺を一つの変数にしてしまいます。こうすると($eE$は定数なので)$-k{\mathrm dv\over\mathrm dt}={\mathrm dX\over\mathrm dt}$となるので、左辺は$-{m\over k}{\mathrm dX\over\mathrm dt}$となります。 -- 前野?
- あとは、$-{m\over k}{\mathrm dX\over\mathrm dt}=X$、つまり${\mathrm dX\over\mathrm dt}=-{k\over m}X$という式を解きます。これの解は$X=C\mathrm e^{-{k\over m}t}$です。 -- 前野?
- あとはこの式を$v=$の形にすれば(5.5)です。 -- 前野?
- 理解出来ました。ありがとうございます。 -- 蔵?
ポインティングベクトル †
物理のひよこ? (2017-09-23 (土) 14:55:23)
今日は、お世話になっています。
p291の図の E × B は、E × H でなくて良いのでしょうか?
- 真空中の話(物質中だとかなりややこしい話になるので本では扱ってない)なので向きはどっちでもかまわないです。上の説明に合わせるとHにすべきですが、本書では基本的な場はEとBだとする立場なので、そっちを使ってます。 -- 前野?
- E × B と E × H とでは,ベクトルの大きさが違うので、エネルギーの流れの大きさも違って来ると思うのですが? --
- ここでは向きだけ表現してると思ってください。実際エネルギーの流量を計算するときはちゃんとやらなきゃいけませんが。 -- 前野?
- 分かりました!有難うございます。ところで、本の内容に関係が無いうえに、著者としてライバル(?)の話で申し訳有りませんが(なので独り言としてスルーで構いません)、先生のような物理マスターから見て「12歳の少年が書いた量子力学の本」をどの様に思いますか?、Amazonのレビューで一部手厳しい評価もあるようですが、自分の様な物理の学習に悪戦苦闘しているような”ひよっこ”からすると、驚愕!の一言で、天才って居るんだな~と唯々感心しきりなのですが(もちろんこの少年が大成するかは分かりませんが)、先生なんかも若い頃からスラスラと物理を理解出来たのでしょうか? -- 物理のひよこ?
p272(相互インダクタンス)について †
物理独学者? (2017-09-04 (月) 23:57:04)
いつもお世話になります。
p272の相互インダクタンスの計算ですが、$I_1$と$I_2$は閉曲線なので、1行目の$\int_{I_2}$は一周積分$\oint_{I_2}$ということかと思います。同様に(11.28)式までの$I_1$および$I_2$上での線積分はいずれも一周積分かと思います。
ところで(以下はコイル同士の関係式ではなくなるので変な考えかも知れませんが)、$I_1$は閉曲線でなくても(電荷溜りA点から、電荷がB点へ流れる状況でも)、その電流が作る磁束が閉曲線$I_2$を貫く場合、(11.27)式より$M_{21}$は求まります。しかしこのとき、$I_1$は閉曲線ではないので、$M_{12}$のほうは考えられず、一般に$M_{21} \neq M_{12}$ではないかと思います。
つまり相互ではなくなりますが、それでも$M_{21}$のことを「相互インダクタンス」と呼ぶのでしょうか。あるいはコイルでないからインダクタンスという概念の範囲を逸脱してしまっているでしょうか。
変な質問ですみません。よろしくお願いいたします。
- 「つらぬく磁束」が定義できない場合はそもそもMを計算する意味がないので、「そんなものは計算しない」、つまりおっしゃる通り「インダクタンスという概念の範囲を逸脱」していると考えるべきだと思います。 -- 前野?
- 分かりました。ご回答いただきましてありがとうございます。 -- 物理独学者?
Faradayの電磁誘導の法則について †
(2017-08-29 (火) 07:09:57)
rotE=-∂B/∂tの解釈についての質問です。
ある本(一冊ではない)には「磁場Bの時間変化が電場Eを作り、また、逆に電場の時間変化が磁場を生み出す」と書かれてあったのですが、別の本の前書きを見ると「それは間違いである」と書かれてあります。
先生の本に目を通したところ、どちらとも書かれておられなかったので質問させていただきました。これはどちらが正しいのでしょうか。
- この問題は「電場の時間変化が磁場を生み出す」という言葉の解釈の問題です。${\rm rot}H=\vec j+{\partial D\over \partial t}$の式を見て考えるならそれは全然間違いではありません。ところがもう一つの${\rm rot}E=-{\partial B\over \partial t}$を使うと磁場に関する二階微分方程式に直すことができて、そちらを見れば電場の時間変化の影響は消えてます。 -- 前野?
- 二階微分方程式の、いわゆる「ソース・ターム」に電場の時間変化が入らないことを「電場の時間変化は磁場を生み出さない」と解釈すれば「それは間違いである」という主張が正しくなります。 -- 前野?
- ${\rm rot}H=j+{\partial D\over \partial t}$の方を見て「電場が時間変化しているその場所では磁場のrotが0ではない」と解釈するのは間違いではありません。 -- 前野?
- こういう、考え方の違いや語義の解釈みたいなややこしい話は、初学者が読む教科書に入れてもしょうがないと思ったので書いていません。 -- 前野?
- 早速の返答ありがとうございます。つまり、「1つ目の式に2つ目の式を代入して整理すると、その解釈は間違いになる」ということでしょうか。 --
- 代入するかどうかなんて関係ないです。代入して間違いなもんなら、代入する前から間違いに決まってます。 -- 前野?
- 上にも書いたことですが「電場の時間変化が磁場を作る」などの言葉をどう解釈するかによって違う、つまりは国語の問題です。物理的にはマックスウェル方程式の中身がわかっていればいいだけのことです。 -- 前野?
- 白黒つけて欲しいと思うかもしれませんが、文章一個だけ切り出して「これが間違いである」とか言える状況ではないです。語義について曖昧なままで「あってますか間違ってますか」と問うのは不毛です。 -- 前野?
演習問題9-3の解答 †
物理独学者? (2017-08-28 (月) 23:31:47)
たびたびすみません。
p27の右上の図(時計回りのほう)で、三角関数の中身のルートの前の符号が違っていますので、お時間がありましたら訂正をお願いいたします。
- ありがとうございます。確かに時計回りと反時計回りが同じになってしまってました。訂正しておきます。 -- 前野?
p293 について †
がじゅ? (2017-08-26 (土) 19:08:35)
p293の内容について質問させて頂きます。
式(12.27)のz微分についてそこからどういう計算をして
式(12.28)のようになるか理解が出来ていない状況です。
宜しければご教授いただけないでしょうか。
- $\epsilon$が定数なので、${\partial D_i\over\partial z}=\epsilon{\partial E_i\over\partial z}$です。 -- 前野?
- ${\partial E_i\over\partial z}E_i={1\over2}{\partial (E_i)^2\over\partial z}$になります($i$は$x,y,z$のどれか)。 -- 前野?
- ご丁寧にありがとうごさいます。やっと理解出来ました。 -- がじゅ?
- ご丁寧にありがとうごさいます。やっと理解出来ました。 -- がじゅ?
一様な磁場中を回転する長さLの導体棒に生じる起電力について †
高校教諭? (2017-08-23 (水) 14:26:05)
高校で物理を教えている者です。よろしければ、電磁誘導に関する疑問点についてお教えください。
一様なBの中でBに垂直に置かれた長さLの導体棒が棒の一端Oを固定してOのまわりを角速度ω
で回転している。このとき、棒は磁束線を横切るので棒に生じる起電力は棒が1s間に横切る磁束線と考えるとV=BL^2ω/2となります。この現象を導体棒の中にある自由電子に注目するとOからの距離がXの自由電子は速さXωで運動しているので、ローレンツ力がeXωB働きます。このため、導体棒の中に電場が生じexωB=eEとなり、E=ωBXとなります。この電場をx=0からLまで積分すると、先に求めた起電力が求められます。以上の内容は物理の問題集などに書いてあります。しかしながら、導体棒のなかの自由電子は円運動しているので、棒の回転による遠心力があるので、ローレンツ力と電場の力がつりあうのではなく、遠心力を加えた力がつり合うと考えられます。こう考えて電場を求めてその電場を積分した値は、棒が1s間に横切る磁束線から求めた起電力と一致しません。この場合、どちらの考え方がよいのでしょうか。
V
- こういう話のとき「電子の向きを変える力はどうなるの?」というのはよく出る疑問ですが、実はたいていの場合「その力は考えなくてもいいくらいに微弱な力です」というのが答えになります。 -- 前野?
- 今の場合だと電子に働く遠心力は$mr\omega^2$ですから、$r$が1m程度、$\omega$が1rad/s程度とすると、電子の質量である$10^{-30}$程度の数です(単位ニュートン)。 -- 前野?
- 一方ローレンツ力$qvB$の方は、$q$が$10^{-16}$程度、$v$はやはり1m/s程度なので、$B$も1T程度だと、$10^{-16}$程度になって14桁も下です(ものすごく大雑把な概算ですが)。 -- 前野?
- 電子の持つ運動量や運動エネルギーは考えている電場や磁場の影響に比べてすごく小さいので、このあたりに神経質になる必要はないわけです。このあたりはp164ページあたりにも書いてます。 -- 前野?
- ・すぐに回答していただき大変ありがとうございます。確かに現実問題として遠心力がローレンツ力に比べて十分小さいことはわかります。もし、仮に電子の質量が(または、導体中で電荷を運ぶ荷電粒子の質量が)大きい場合は、回転する導体棒に生じる起電力の計算は遠心力を考慮しないといけないのでしょうか。その場合は、棒に生じる起電力は棒が単位時間に横切る磁束線である、という考えは成り立たなくなるのでしょうか。 -- 高校教諭?
- そういう意味では、磁場がなくても回転させれば(あるいは単純に重力があるだけでも)電位差は発生していることになります。「棒に生じる起電力」を、「磁場によって起こる起電力」と解釈するなら、磁場がなくても発生している電位差は差っ引いて考えるべきだと思いますので「電磁誘導によって生じる起電力は棒が単位時間に横切る磁束である」というのは間違ってないことになります。 -- 前野?
- 丁寧にご返答いただき大変ありがとうございます。おかげで、私の疑問は解消されました。 -- 高校教諭?
p169の上図について †
物理独学者? (2017-08-17 (木) 23:24:02)
頻繁に投稿してすみませんが、質問をさせてください。
p169の上図(スイッチを閉じる前の図)の状況は分かりましたが、回路を繋げてこの状況になるまでの経緯が気になり、以下のように考えてみました。
導線はスイッチのところで分離しているので、これから電池のプラス極に繋げる導線をAとし、同様にマイナス極に繋げる導線をBとします。
この状態ではまだ導線A、Bとも電池と繋がっていないので、周囲の空間と等電位になっています。(自由電子がランダムに運動していると思います。)
次に導線Aを電池のプラス極に繋げます。このとき導線Aの電位は電池のプラス極と等電位になります。導線Bはまだ電池と繋がっていないので、依然として周囲の空間と等電位になっています。(※1)
次に、導線Bを電池のマイナス極に繋げます。このとき導線Bの電位は電池のマイナス極と等電位になります。そして、導線Aと近接しているスイッチのあたりで電位差が生じ、そのため自由電子が力を受け、「小さなコンデンサ」を形成します。これで、p169の上図の状況となります。
以上の考えにおかしいところはないでしょうか。
なお、文中※1のところでは、導線Bの電位と、導線Aの電位との間に電位差があるでしょうから、この時点で既に何らかの「小さなコンデンサ」になっていると考えるべきでしょうか。
初歩的なことと思いますが、よろしくお願いします。
- その考え方で問題ないです。 -- 前野?
- 分かりました。ご回答いただきまして、ありがとうございます。 -- 物理独学者?
演習問題4-2の解答 †
物理独学者? (2017-08-13 (日) 23:18:22)
たびたびすみません。
下から3行目の$D'_{\parallel} = \frac{\epsilon_0}{\epsilon} D_{\parallel}$は、$D'_{\parallel} = \frac{\epsilon}{\epsilon_0} D_{\parallel}$だと思います。よろしくお願いします。 -- 物理独学者?
- すいません、確かに分母分子が逆でした。近日中に修正しておきます。 -- 前野?
- ありがとうございます。ついでに演習問題4-3の解答の() -- 物理独学者?
- →続き (E.50)式の球内部の$\vec{D}$の式の分母が$3_0$と誤植になっていますので、訂正をお願いします。 -- 物理独学者?
- すいません、これも近日中に直します。 -- 前野?
- すみません、p166の下から12行目「C地点はD地点に比べ」は、「D地点はC地点に比べ」かと思います。よろしくお願いします。 -- 物理独学者?
- 確かにCとDが逆でした。 -- 前野?
演習問題3-6の解答 †
物理独学者? (2017-08-12 (土) 01:16:14)
いつもお世話になります。
p17の下から2行目の$V(r)$は$V(r,\theta)$だと思います。
同様にp17の下から1行目の$V(r)$は$V(r,\theta,\phi)$だと思います。
また、(E.37)式の最後の行で、カッコの前は$\frac{p\cos{\phi}}{4\pi\epsilon r^4}$だと思います。よろしくお願いします。
- 上でもつけてないので、むしろ(r)がいらなかったですね、すみません。 -- 前野?
- (E.47)の最後も、たしかに分母は$4\pi\varepsilon_0 r^4$ですね。 -- 前野?
問い8-1 †
phys? (2017-08-11 (金) 11:17:27)
問い8-1について質問です。解答を熟読して計算もしてみましたが、解答p319の1番下の式で、第1項の部分積分の仕方と、第2項をどう変形したらdiv$\vec{H}$が出てくるのかが分からないです。特に第1項に関して、左側のナブラは、$\vec{H}$の右側にあるのに、$\vec{H}$を微分するのですか??
- 第1項の左の$\vec\nabla'$($\vec A$)はもともと左辺の$\vec\nabla'\times\vec H$の$\vec\nabla'$なのですから、微分は$\vec H$に掛からなくてはいけません。そういう計算をやらないとおかしなことになります。 -- 前野?
- 通常とは違う表記ですが、そういう特別な書き方をしていると思ってください。 -- 前野?
- 部分積分は、単純にこの$\vec A$に対応する$\vec\nabla'$を前($\vec H$)ではなく後ろに掛けます。$\vec\nabla$だとわからないのなら、${\partial \over\partial x},{\partial \over\partial y},{\partial \over\partial z}$に分けて考えてみてください。 -- 前野?
- 第2項については、$\vec C$の部分にある$\vec\nabla'$を部分積分して$\vec H$の方に掛ければdiv Hになります。 -- 前野?
- わかりました。ありがとうございました! -- phys?
p130 問い3-3 †
物理独学者? (2017-08-09 (水) 23:57:07)
いつもお世話になります。
下の方のご質問とも関連すると思いますが、問い3-3で面に働く張力が$\frac{q^2}{16 \pi \epsilon_0 L^2}$であるということは、この面は作用反作用の法則により、その張力と同じ力で周囲の電気力線(ゴム紐)を引っ張る。だからその力(異符号電荷間のクーロン力)は引力である、という理解でよいでしょうか。
よろしくお願いします。
- もちろん、静電気学でも作用反作用の法則は成り立ちます。 -- 前野?
- 力を及ぼし合うのは「電気力線」や「面」ではなく、下の答えに書いたような「□でくくった空間の一部」が「隣(上下作用前後にある)の空間の一部」との間に力を及ぼしあっている、と考えた方がいいと思います。電気力線は「電場を表現する線」で実体あるものではないので。力を及ぼし合うのは空間という実体で、力の作用点は空間と空間の境界です(境界と言っても何かで区切られているわけではない)。 -- 前野?
- なるほど、ありがとうございます。「電場$\vec{E}$が存在する微小空間」は、「その周囲の微小空間との間に(3.103)式で表される応力を及ぼしあう弾性体」とみなすことができる(その様子を示したのが下図)と理解しました。 -- 物理独学者?
電場の応力 †
phys? (2017-08-07 (月) 23:29:04)
電場の応力について質問させていただきます。
p128で、12行目から13行目の力の向きだと電場の「短くなろうとし、混雑を嫌う」性質と真逆の方向を向いているのではと思ったのですが、いかがでしょうか。
($d\vec{S}$は面に垂直で外側を向く面積ベクトルなのでしょうか。)
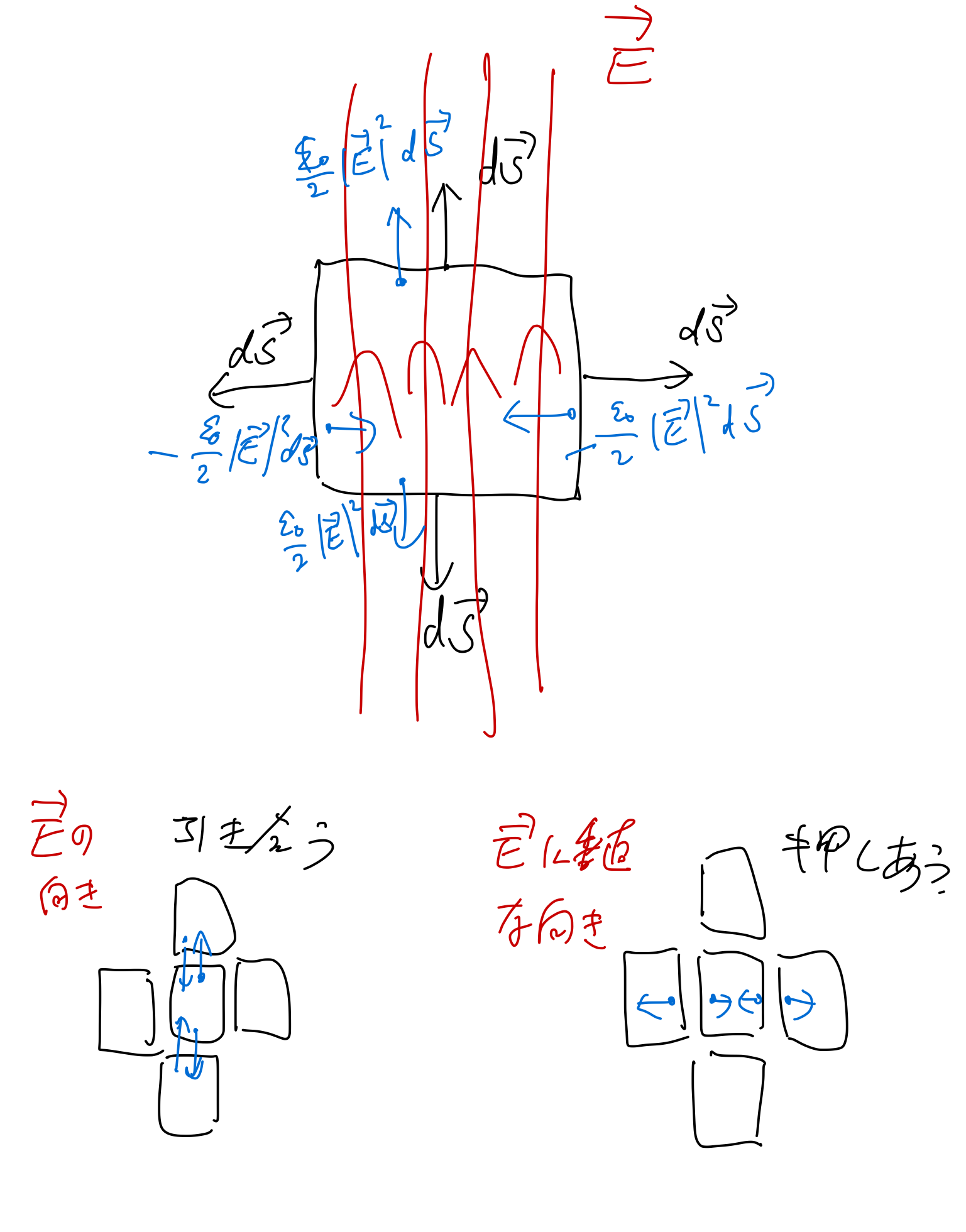
- 図で描くと上のような感じです。$\mathrm d\vec S$は外に向かうベクトルです。 -- 前野?
- 微小面積どうし引き合ったり押し合ったりして、結果的に考えている面積全体で電気力線が短くなったり混雑を避けたりするということでしょうか? -- phys?
- どうしても、p127の図をみると$\vec{E}$と$\vec{S}$が平行な時は下向きに(ひもが短くなろうとするように)力がかかるのではと思ってしまいます。 -- phys?
- 図の下にある十字に並んだ正方形の真ん中の正方形の気持ちになって考えて下さい。 -- 前野?
- 「引き合う」の場合、自分の上(天井)g上向きの、下(床)が下に力を受けます。これは引っ張られているということです。 -- 前野?
- これは「伸びたゴム紐」と同じ状況です。 -- 前野?
- p127の16行目に「xが増える方向の反対」に張力が生じるとあります。今の御説明だと、真ん中の正方形は、「xが増える方向」に力を受けることになるのではないでしょうか? -- phys?
- 「押しあう」の場合でも同様に、電気力線が広がろうとするのではなくその逆の縮もうとする方向に、真ん中の正方形は、力をうけているのではないでしょうか。 -- phys?
- 「押しあう」の場合でも同様に、電気力線が広がろうとするのではなくその逆の縮もうとする方向に、真ん中の正方形は、力をうけているのではないでしょうか。 -- phys?
- 「押し合う」の場合、この力の結果、正方形が押しつぶされる方向の力です。これは両サイドから押されているわけで満員電車などと同様の状況です。 -- 前野?
- 力の向きはその逆じゃないといけないのではないですか? -- phys?
- 押しつぶされれば電気力線は混雑すると思うのですが。 -- phys?
- 回りの電気力線が、混雑を嫌って私を押しているのです。そして私は混雑を嫌って両サイドを押してます。 -- 前野?
- なるほど!そして面全体では広がるのですね? -- phys?
- 「面全体では」の意味がよくわからないけど、最終的にはいろんな場所に働いた力のバランスが取れた(釣り合った)状態に落ち着いて終わります。 -- 前野?
- バランスのとれた(つりあった)状態では、$\vec{E}$と$\vec{S}$が平行のときは初めより力線が短くなり、$\vec{E}$と$\vec{S}$が垂直のときは初めより力線の混雑が緩やかになる、これは合っていますか? -- phys?
- 始めと今を比較する意味はないです。実際に何かが動くわけじゃないし、電気力線も、初めの線と今の線に対応関係があるわけじゃないので。そもそも「始め」というのがどういう状況なのかを定義しないとなんとも言えない感じです。 -- 前野?
- わかりました。疑問点がわかりとても嬉しいです。ご丁寧な回答ありがとうございました! -- phys?
p73、p54 †
物理独学者? (2017-08-05 (土) 15:05:25)
いつもお世話になっています。
p73の本文中、上から2行目の$V_r$は$E_r$、同じく3行目の$r^2 V_r$は$r^2 E_r$の誤植かと思います。
あと些末ですが、p54の下から7行目の「電場$\vec{E}$」の後ろに$=$が抜けています。
よろしくお願いします。
- 演習問題2-1の解答で、$\rho < \rho_1$のとき、$E(r)$とあるのは$E(\rho)$と思います。 -- 物理独学者?
- 演習問題2-4の解答で、(E.12)式の2行目の最後の$=0$は、まだ計算が続いているので不要と思います。 -- 物理独学者?
- p81の脚注4の1行目で、「万有引力」のうしろに$-$が抜けています。 -- 物理独学者?
- いろいろ御指摘ありがとうございます。訂正しておきます。 -- 前野?
- 81ページの万有引力は「万有引力の大きさ」と訂正しておきたいと思います(大きさを見ると同じ式だが、向きが違うのでエネルギーの式は変わるということを説明したい部分なので)。 -- 前野?
p47 本文中程の式について(再掲) †
物理独学者? (2017-07-30 (日) 22:14:57)
計算を間違えていたので再掲させてください。
p47の中程、「微小面積は$\mathrm d S = n_x\mathrm d y\mathrm d z + n_y\mathrm d z\mathrm d x + n_z\mathrm d x\mathrm d y$」とありますが、これは以下のように理解してよいでしょうか。
「いま例として$\vec{n}=(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})$の微小面積を考える。$\mathrm d z = \frac{1}{\sqrt{3}}$とする。また$\mathrm d x = \mathrm d y$とすれば、$\mathrm d x = \mathrm d y = \frac{-1+\sqrt{7}}{\sqrt{3}}$と決まる。この例に限らず、あらゆる$\vec{n}$において、$\mathrm d x$か$\mathrm d y$か$\mathrm d z$のいずれか1つを決めることにより、上式を満たす$\mathrm d x,\mathrm d y,\mathrm d z$の組が決まる」
よろしくお願いします。
- $\vec{n}=(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})$です。ぐだぐだですみません。 -- 物理独学者?
- 「$\mathrm d x = \mathrm d y = \frac{1}{\sqrt{3}}$と決まる。」です。また計算を間違えていました・・。あと、$\mathrm d S = 1$として計算しています。 -- 物理独学者?
- $\mathrm dx$などは微小量ですから、${1\over\sqrt{3}}$のような数値を与えることはそもそもできません。 -- 前野?
- もちろん、$\mathrm dS=1$と置くことにも意味はありません。$\mathrm dS$には数としての意味はなくて、$\int \mathrm dS$のような積分を行って初めて数になります。 -- 前野?
- だからたとえば、$\vec n$が$z$方向を向いているときなら、$\int_0^{L_x} \mathrm dx\int_0^{L_y}\mathrm dy$のような積分をして初めて意味のある面積という量$S=L_xL_y$になります。$\mathrm dS={1\over\sqrt{3}}(\mathrm dy\mathrm dz+\mathrm dz\mathrm dx +\mathrm dx\mathrm dy+\mathrm dz$の場合なら、この三つの項をそれぞれについている$\mathrm dx$などに関して積分を(それぞれ二回)行って初めて数になります。 -- 前野?
- とにかく、$\mathrm dx$という記号の意味は「微小量」であるという意味がわかってないと、この式の意味は理解できないと思います。 -- 前野?
- ご回答ありがとうございます。この式は直感的に分からなかったので、図を描いて考えていたのですが、微小量ということを見失ってしまいました。改めて、次のように考えなおしてみました。 -- 物理独学者?
- $\mathrm d S$を閉曲面$S$全体に渡って積分すると、$\int_S \mathrm d S = \int_S \vec{n} \cdot \vec{n} \mathrm d S = \int_S (n_x n_x \mathrm d S + n_y n_y \mathrm d S + n_z n_z \mathrm d S)$となる。 -- 物理独学者?
- 右辺第1項のうち$n_x \mathrm d S$は、$\mathrm d S$を$yz$平面に射影したものなので、それを$S$全体に渡って積分するということは、$\int_S \mathrm d y \mathrm d z$とイコールである。(このとき$S$は風船を$x$方向につぶしたような閉曲面になっていて、その面上で微小面積$\mathrm d y \mathrm d z$を足し上げる。) -- 物理独学者?
- $xy$平面、$zx$平面においても同様であるので、$\int_S \mathrm d S = \int_S (n_x \mathrm d y \mathrm d z + n_y \mathrm d z \mathrm d x + n_z \mathrm d x \mathrm d y)$となる。ゆえに、p47中程の式が導かれる。 -- 物理独学者?
- 以上の考えで正しいでしょうか。よろしくお願いいたします。 -- 物理独学者?
- まず最初の$\vec n\cdot\vec n$ってのは何でしょう?? この変な計算をしなくても、$\mathrm d S$のうち$\mathrm dy\mathrm dz$に比例する部分を取りだせば「$yz$平面に射影したもの」が出てくるのですが。 -- 前野?
- ああすいません、$\mathdm d\vec S=\vec n\mathrm dS$のような書き方をしたかったということでしょうか。そう考えなくても、$\vec n=n_x\vec {\mathbf e}_x+n_y\vec{\mathbf e}_y+n_z\vec{\mathbf e}_z$と$\mathrm d\vec S=\mathrm dy\mathrm dz\vec{\mathbf e}_x +\mathrm dz\mathrm dx\vec{\mathbf e}_y + \mathrm dx\mathrm dy\vec{\mathbf e}_z$と内積を取ったと思えばすぐに結果は出ます。 -- 前野?
- お手を煩わせてすみません。$n_x$をあらわに2つ出すことを意識したのでそのような書き方になってしまいました。 -- 物理独学者?
- ただ、そもそも微小面積であるがゆえにp47の上の3つの図より、一般の$\mathrm d\vec{S}=\mathrm d y\mathrm d z\vec{\mathbf e}_x + \mathrm d z\mathrm d x\vec{\mathbf e}_y + \mathrm d x\mathrm d y\vec{\mathbf e}_z$と書けるわけなので、そこから直ちに$\mathrm d S = \vec{n} \cdot \mathrm d\vec{S} = n_x \mathrm d y \mathrm d z + n_y \mathrm d z \mathrm d x + n_z \mathrm d x \mathrm d y$が出てくることがよく分かりました。 -- 物理独学者?
- ベクトル解析(面積分)も併せて勉強していく必要性を感じました。ありがとうございます。 -- 物理独学者?
p47 本文中程の式について †
物理独学者? (2017-07-30 (日) 22:08:09)
度々の質問ですみません。
p47の中程、「微小面積は$\mathrm d S = n_x\mathrm d y\mathrm d z + n_y\mathrm d z\mathrm d x + n_z\mathrm d x\mathrm d y$」とありますが、これは以下のように理解してよいでしょうか。
「いま例として$\mathrm d z = \frac{1}{\sqrt{3}}$とし、また$\mathrm d x = \mathrm d y$とすれば、$\mathrm d x = \mathrm d y = \frac{-2+\sqrt{7}}{2\sqrt{3}}$と決まる。この例に限らず、あらゆる$\vec{n}$において、$\mathrm d x$か$\mathrm d y$か$\mathrm d z$のいずれか1つを決めることにより、上式を満たす$\mathrm d x,\mathrm d y,\mathrm d z$の組が決まる」
よろしくお願いします。
p40 本文9行目 †
物理独学者? (2017-07-29 (土) 01:36:46)
お世話になります。
些末なことですが、立方体 は 直方体 ですよね。
よろしくお願いします。
- すみません、もう一つ。演習問題1-2のヒントで、「その球殻に単位面積あたり$\rho$の電荷があるということは、単位面積あたり$\rho dr$の電荷があるということ」は、「その球殻に単位面積あたり$\sigma$の電荷があるということは、単位体積あたり$\rho dr$の電荷があるということ」ではないでしょうか。よろしくお願いします。 -- 物理独学者?
- すいません、この二箇所は確かにミスしてます。 -- 前野?
- 「その球殻に単位体積あたり$\rho$の電荷があるということは、単位面積あたり$\rho\mathrm d r$の電荷があるということ」が正しいです。 -- 前野?
- ありがとうございます。二つ目は勘違いしていました。 無限に薄い($dr$→$0$)球殻は球面とみなせるので、単位面積あたり$\sigma$(=$\rho dr$)の電荷があるということは、単位体積あたり$\rho$の電荷があることと等価ですね。 -- 物理独学者?
gradVの向き †
やま? (2017-07-27 (木) 00:31:42)
2度もすみません
P87の電位はV(x,y)で表されていると思いますが、このとき、ベクトルgradVの向きは勾配が最も急な方向を意味すると書かれています。
この向きは、平面的(zベクトルを含まない)な方向でしょうか?
勾配というと図の斜面に沿った方向をイメージしそうになります。
- v(x、y)と書いている場合、z方向は全く考えてません。この場合の「高さ」に当たるものは電位vという「架空の方向」です。vという架空の方向と実在の方向(ただし今は考えてない)をごっちゃにしてはいけません。 -- 前野?
- そもそもgradの定義の中に「vの方向」の成分は入ってませんね。 -- 前野?
- ということはz(x,y)と書くと斜面に沿った方向を向くのですね。 -- やま?
- では、3変数関数Φ(x,y,z)は架空の方向Φがあるため同様に斜面に沿った3次元ベクトルになるのですか? -- やま?
- $z(x,y)$のgradは$\vec{\mathbf e_x}{\partial z(x,y)\over\partial x}+\vec{\mathbf e_y}{\partial z(x,y)\over\partial y}$です。$z$方向は向きません。定義通りに考えましょう。 -- 前野?
- 3変数関数の場合も定義に沿って考えましょう(適当なフィーリングで考えてはいけない)。gradは$\vec{\mathbf e_x}{\partial \Phi(x,y,z)\over\partial x}+\vec{\mathbf e_y}{\partial \Phi(x,y,z)\over\partial y}+\vec{\mathbf e_z}{\partial \Phi(x,y,z)\over\partial z}$です。これは「3次元空間の中のある1方向を向いたベクトル」ですが「斜面に沿って」なんて要素はどこにもありません(そもそも斜面って何?)。 -- 前野?
- 斜面に沿った方向とはp86の下図の矢印をイメージしていて、この方向がgradだと思っていました。 -- やま?
- もう1度じっくりと読み直してみます。ありがとうございました。 -- やま?
gradの意味について †
やま? (2017-07-22 (土) 21:57:33)
gradについて質問です。
p86に、ある方向(eベクトル)にh離れた場所との比較と書かれています。
ただ、p87の電位については、gradVの向きは勾配が「最も急」な方向を意味すると書かれています。
これはgradが最も急な方向について定義されているという事でしょうか?
- p86の説明では、最も急な方向に限定していないので悩んでしまいました -- やま?
- 定義どうりに計算すればgradは自動的に最も急な方向を向きます。 -- 前野?
- そういうことでしたか ありがとうございます -- やま?
p140 導体球 †
ぬらりひょん? (2017-07-02 (日) 00:23:28)
導体球の電位を、内部に電気双極子があると仮定したものと同じになるロジックがよく分かりません。
確かに計算して見ると、導体の境界における接続条件から電気双極子と繋がるのが確認できました。ところが、上手く境界で滑らかに繋がる関数を探せば、必ずしも内部に電気双極子がある としなくても良いような気がします(頑張って探しましたが、結局見つかりませんでした)。
P.S. 物理数学の新刊、出版 おめでとうございます! いつも前野さんの教科書を頼りに勉強してます笑
- その前のページに書いてありますが、境界条件を正しく満たすようなポアッソン方程式の解は一つしかありません。よって境界条件を満たすような解が一つあれば「他にもあるのでは」と心配する必要はない(というか、他に見つかってしまったら計算を間違えている)ということになります。 -- 前野?
これより古い記事は
にあります。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)