「今度こそ納得する物理・数学再入門」(技術評論社)サポート掲示板 †
今度こそ納得する物理数学再入門サポートページに戻る
p79 †
物理独学徒? (2023-03-08 (水) 21:01:24)
連投すみません。p79の下から2つ目の数式、第1項の偏微分は$\frac{\partial^2 f}{\partial x^2}$かと思います。
- これもご指摘のとおりです。次の版で訂正したいと思います。 -- 前野?
- 下の件も併せてご回答ありがとうございます。よろしくお願いいたします。 -- 物理独学徒?
p76 †
物理独学徒? (2023-03-08 (水) 20:52:48)
p76の3行目は$\frac{\partial}{\partial \phi} \vec(e)_\phi = -cos\phi \vec(e)_x-sin\phi \vec(e)_\phi$ではないでしょうか。
- p76の3行目は$\frac{\partial}{\partial \phi} \vec e_\phi = -cos\phi \vec e_x-sin\phi \vec e_\phi$ではないでしょうか。 -- 物理独学徒?
- 度々すみません。p76の3行目は$\frac{\partial}{\partial \phi} \vec e_\phi = -cos\phi \vec e_x-sin\phi \vec e_y$ではないでしょうか。 -- 物理独学徒?
- すいません、ご指摘の通りです。 -- 前野?
p53(gradの意味) †
物理独学徒? (2023-03-05 (日) 23:32:17)
第5刷を使っています。
p53(gradの意味)の6行目で、「・・・関数$(x,y,z)$の差を取る。」とありますが、これは「・・・関数$\phi(x,y,z)$の差を取る。」でしょうか。
しっかり分かっていないので、間違えていたらすみません。
- すいません、これはおっしゃるとおり、$\phi$が落ちてます。 -- 前野?
- ご回答ありがとうございました。引き続き勉強します。 -- 物理独学徒?
ご確認を †
yougoemon? (2018-08-04 (土) 07:04:37)
図書館で借りて読んだので、第1刷を読みました。
・第1刷のP181 上の図の青い矢印がx軸反対方向との記述がP181 1行目にありますが、青い矢印の向きが合っていないのではないでしょうか?それともP181の図は、p180の下の図と座標の設定が異なっているのでしょうか?
・第1刷のP192 11行目の「p=Ec」は正しくは、「p=E/c」ではないでしょうか
- p181の図についてはこれであってます。3D図が見にくいのかもしれませんが、青い矢印は「こちらがわからむこうがわへ」の方向になってます。 -- 前野?
- p192については、すいません、確かに間違ってます。次の刷があれば訂正します。 -- 前野?
- お忙しい中、早速の回答有り難うございました。引き続き他の著書も拝読させて頂きます。 -- yougoemon?
p63 †
zx? (2018-02-28 (水) 18:07:28)
上から5行目の式は全微分になっていますが、偏微分ではないでしょうか?
よく理解していないので、違ったらすみません。
- ああ、これは印刷のミスです。すみません。 -- 前野?
- お答え頂き、ありがとうございます。 -- zx?
p42 †
zx? (2018-02-28 (水) 17:00:58)
p42の一番下の左辺はそれぞれ、
det(a_x b_x と、det(a_x c_x
a_y b_y ) a_y c_y)
ではないでしょうか?
見にくい表記ですみません。
- detの計算をすればどっちでも同じになるので本の通りでも構いませんが、そこまでの説明からすると御指摘のように書いた方がよいですね。 -- 前野?
- お答え頂き、ありがとうございます。 -- zx?
p140の右上の図 †
物理独学者? (2017-05-06 (土) 15:02:07)
p140の右上の図で、$Q=\frac{\Delta S}{T}$となっていますが、正しくは$Q=T\Delta S$かと思います。よろしくお願いします。
- 確かに間違ってますね、ごめんなさい。書きたかったのは$\Delta S={Q\over T}$でした。 -- 前野?
- ご回答ありがとうございました。 -- 物理独学者?
p64の上の図 †
物理独学者? (2017-02-20 (月) 21:52:27)
p64の上の図で、x方向は下に凸なので$\frac{\partial^2}{\partial x^2}V > 0$となり、y方向は上に凸なので$\frac{\partial^2}{\partial y^2}V < 0$となり、足すと打ち消しあって$0$になる、ということですよね。よろしくお願いします。 -- 物理独学者?
- はい、その通りです。図に描いてあるのはおかしくて、足して0です。 -- 前野?
- ご回答ありがとうございました。 -- 物理独学者?
双子のパラドックスの解決 †
黄昏に帰る? (2016-04-14 (木) 15:59:30)
P208の図で、Pとqの点は同時と言っていますが、これは兄の座標系の話です。弟の座標系では同時の相対性により、兄の座標系で異なる座標の時刻、P,qが異なるのは当然であり、P点の時刻はq点の時刻とは言えません。
それにもまして、時空図の作成定義から、P点のイベントを弟の座標系で見た時刻はPから水平に引いた線とt軸との交点です。ジャンプなどあり得ません。
- 正確には、Pとqが同時なのは「行きの兄にとっての座標系」ですね(それは本にも明記してあります)。弟からみるとPとqは同時ではありませんが、行きの兄の座標系にとってはPとqが同時です(それが「同時の相対性」ですね)。 -- 前野?
- 弟から見た「P点と同時」は「Pから水平に引いた線とt軸の交点」なのはおっしゃる通りです。本で説明している「ジャンプ」というのは「行きの兄」と「帰りの兄」の座標系の乗り換えのときの話で、これは兄にとっては「あり得る」話です。 -- 前野?
- 正直、対応していただいて感激しています。 -- 黄昏に帰る?
- 兄の異なる座標の同時を弟の一点の時刻にまとめているのが誤りと思います。そして、基本は片道でも本質の議論はできます。座標の乗換の議論では時計を取り換えています。始めの時計を一緒に持って行ったとき、反転でどうなるかはわからないのです。 -- 黄昏に帰る?
- 「弟の一点の時刻でまとめている」という意味がよくわからないのですが、兄に関しては「座標を乗り換える」という操作を実際行ってます。そのとき「時計が反転でどうなるかはわからない」なんてことはありません。図では簡単にするために一瞬で加速を終わらせてますが、実際には速度は連続的に変化するものだから、時計もそれに応じて連続的に変化します。 -- 前野?
- ここの議論は無理なので止めます。もし出版の予定がありましたら是非、考えて欲しいと思います。調べたところ、シュッツが出所で、その弟子・訳者と仲良しGが日本に広めたらしい。あと、座標の乗換で、帰りの時間もP点は同様に水平に線を引かねばなりません。そして、乗り換えた座標の時計はその前の座標の時計とは無関係にそれぞれ時計がリセットされており、時計の連続性は無い。先生の書籍は昨今の目的不明なものより、「志」が感じられ、好感がもてます。 -- 黄昏に帰る?
- ここの議論は無理なので止めます。もし出版の予定がありましたら是非、考えて欲しいと思います。調べたところ、シュッツが出所で、その弟子・訳者と仲良しGが日本に広めたらしい。あと、座標の乗換で、帰りの時間もP点は同様に水平に線を引かねばなりません。そして、乗り換えた座標の時計はその前の座標の時計とは無関係にそれぞれ時計がリセットされており、時計の連続性は無い。先生の書籍は昨今の目的不明なものより、「志」が感じられ、好感がもてます。 -- 黄昏に帰る?
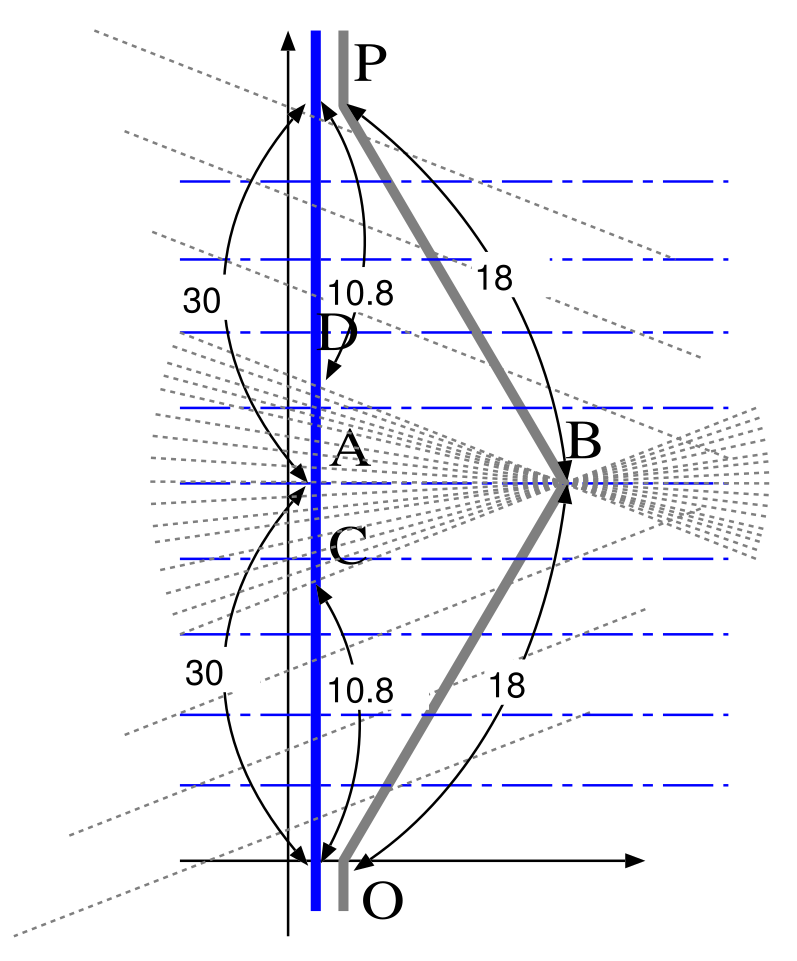
- 209ページの図を一瞬でなく連続的な加速に書きなおしたものが↑の図です。ちゃんと連続歴な加速を行なう場合を考えれば、時間の不連続性はどこにもありません。 -- 前野?
- 連続的な加速(速度の変化)にともなって、兄にとっての同時刻線が連続的に変形されていく、という話ですから、「時計のリセット」などということはどこでも起こっていません。 -- 前野?
- リセットはP点で時刻合わせをしたのでリセットしたという意味でした。しかし、話を広げたのでここは無視してください。要はP点から水平に引いた交点が弟の時刻です。宇宙船は1点としていますが、長い宇宙船を考えたら、q点は兄ではなく宇宙船の後ろにいる誰かの時間になります。先生と議論できる力は無いので止めたいと思います。 -- 黄昏に帰る?
rotとAmpèreの法則について †
もと? (2016-03-19 (土) 14:37:22)
rotがベクトルだという事をAmpèreの法則と絡めて言うと、電流密度j(x,y,z)のz成分jzと「xy平面に平行に単位磁極を(任意のループで)移動させたときに磁場がした仕事(xy平面に対して常に平行に移動させたと考えています)」
つまり、磁場Hと電流Iが直行しているという関係(フレミング左手の法則)が成り立っているということでしょうか。
よくわかる電磁気学のサポートページでrotはAmpèreの法則のために作られたのですか?という質問をされている方がいらっしゃったのでその考えで考えてみたのですが。
- どうも質問の意味が読み取れないのですが、アンペールの法則は、「z成分」とか「xy平面に平行に」などのように条件をつけたら成立する式ではなくて、どんなループでも(立体的な動きをしたってよいのです)成り立つし、電流も「面を貫く」電流でありさえすればどう流れてようが成立ちます。 -- 前野?
- すみません。平行の部分は削除したつもりだったのですが…。 -- もと?
- 電流密度j(jx,jy,jz)のjzと等しいのは単位磁極を任意のループで(先生の仰る通り立体的に移動させてもよいので立体的に移動させると) -- もと?
- jzに等しくなるのが(1周した時のxy平面での移動距離)×磁場強度になるということでしょうか。 -- もと?
- すみません、使い方がいまいちわからなくて文が幾つかに分かれてしまいました。xy平面での移動距離というのは、今、立体的に移動させていると考えているので(例えば、教科書などではxy平面に平行にループさせているものが多いですが、それを斜め向けた場合など)はx方向にトータルで〜だけ移動した、y方向に〜、z方向に〜というように考えて、x方向の移動距離×磁場強度+y方向の移動距離×磁場強度という意味です。 -- もと?
- 立体的に移動させる場合、『貫く電流』はjzだけでは決まらないです。あと単なる(距離)×(磁場)ではなく線積分をしないとダメですね。 -- 前野?
- どういうふうにループをとっても、$\oint \mathrm d\vec x\cdot \vec H=\int \mathrm d\vec S\cdot \vec j$という計算をマジメにやればいいのであって、それがxy平面なら右辺は$j_z$の積分に自動的になります。 -- 前野?
rotの向きについて †
さけ? (2014-11-24 (月) 15:27:09)
rotがベクトル場の回転を表すというのは、よく分かったのですが、rotの向きは、右ねじの進む方向ですよね?
これは、どういうイメージを持てば良いのでしょうか?
- えっと。イメージとしてはまさに「右ねじの進む方向」なのですが、その上にどういう意味でイメージを持ちたいのでしょう??角運動量にしろ何にしろ、このような回転を表現するベクトルの向きは「回転軸」というイメージで考えるしかないと思いますが。 -- 前野?
- お返事ありがとうございます。rotの回転がネジをくるくる回す事だとして、それから生じるベクトルがrotの計算によって出てくるベクトルという認識でいいのでしょうか?回転しているのに、なんで回転軸の方へ進むのか?がイマイチしっくり来なくて質問しました。意図がよく伝わっていなかったようですみません。 -- さけ?
- お返事ありがとうございます。rotの回転がネジをくるくる回す事だとして、それから生じるベクトルがrotの計算によって出てくるベクトルという認識でいいのでしょうか?回転しているのに、なんで回転軸の方へ進むのか?がイマイチしっくり来なくて質問しました。意図がよく伝わっていなかったようですみません。 -- さけ?
- rotの示すベクトルには「進む」というイメージはありませんから、そういうイメージを持ってはいけないと思います。あくまで「軸の方向を示す(大きさが回転の強さを表す)ベクトル」でしかありません。「進む」という意味を持たせてはいけないし、実際進んだりしてないわけです。 -- 前野?
- お返事がかなり遅くなりすみません。「大きさが回転の強さを表す」という一言でしっくり来ました。ありがとうございます。 -- さけ?
P33 の図について †
kei? (2014-05-12 (月) 23:09:40)
なぜ、青い矢印が連結されて、元の位置に戻らなければならないのでしょうか。
- この図は、x,y,zの三つの間にある関係(f(x,y,z)=0のような)がある場合の話です(そうでなくて、x,y,zが全部独立なら偏微分すれば0です)。x,y,zの3次元で、一つの関係式があるので、取り得る値は2次元、つまり面の上にしかないことになります。図の三角形はその「取り得る面」の上にあるわけです。 -- 前野?
- ご教示ありがとうございました。局所的な微小領域では、f(x,y,z)=0等の曲面が平面とみなせるので、図のような三角形を想定して、一般的な関係式を導出できるということですね。 -- kei?
P.73 e_r新の式について †
kero? (2014-03-22 (土) 23:30:16)
基本的な質問ですみません。
e_r新=cosΔθ*e_r旧 + sinΔθ*e_θ旧の式の出し方ですが、もっと詳しくご説明いただけませんでしょうか?
P.73右上の図を見て、なぜそうなるのかが理解できませんでした。
- 図を見れば、「$\vec e_{r新}$という長さ1のベクトルが直角三角形の斜辺になっていて、底辺と高さがそれぞれ長さcosΔθとsinΔθ、向きが$\vec e_{r旧}$と$\vec e_{θ旧}$という形になっている」ことがわかります。わからないのは「こういう図になるのがわからない」のか「この図からこの式がなぜ出てくるのかわからない」か、どっちでしょう?? -- 前野?
- なぜこういう図になるのかというと、結局のところ$\vec e_{r新}$と$\vec e_{r旧}$がθだけ傾いているから(そして$\vec e_{θ旧}$はそれに垂直だから)、ということになります。 -- 前野?
- 図から式を読み取るには、「$\vec e_{r新}$の方向に1進む」という移動は「$\vec e_{r旧}$の方向にcosΔθ進んで、$\vec e_{θ旧}$の方向にsinΔθ進む」という移動と同じ移動になっている、というベクトルの足算を読み取ればよいです。 -- 前野?
- 早速のご回答ありがとうございます! 「こういう図になるのがわからない」が質問の意図です。 あいまいな質問をしてしまい申し訳ないです。 -- kero?
- やっと理解できました。 P.73右上図で$\vec e_{r新}$の根元を$\vec e_{r旧}$の根元に移動したら、すんなりと理解できました。ありがとうございます。 -- kero?
- その後の式展開についても質問させてください。$\vec e_{r新}$ - $\vec e_{r旧}$ = (cosΔθ-1)$\vec e_{r旧}$ + sinΔθ$\vec e_{θ旧}$ / Δθ となります。 lim[Δθ→0]cosΔθ = 1なので(cosΔθ-1)$\vec e_{r旧}$ / Δθ = (1 - 1)$\vec e_{r旧}$ / Δθ = 0という理解でよろしいでしょうか? 分母にΔθがあるのにcosΔθだけ先に極限をとってしまってもよいのでしょうか? -- kero?
- Δθが小さい時、$\cos\Delta\theta\simeq 1-{1\over2}(\Delta \theta)^2+\cdots$となりますから、$\cos\Delta\theta-1\simeq -{1\over2}(\Delta\theta)^2+\cdots$となります。つまり、分子の方はΔθの2次のオーダー、分母はΔθの1次のオーダーなので、分子の方がより小さく、極限は0になります。 -- 前野?
- なるほどです。 級数展開ですね。納得です。 cosΔθ-1/Δθのグラフをエクセルで描いてみたら確かに0に近づいています。 -- kero?
- 追加ですみません。P.77の上から13行目に”右の図のように考えると”とありますが、これはP.77の右上の図を指しているのでしょうか? -- kero?
- はい、そうです。配置的には「右の」というよりは「上の」になってしまってますね。 -- 前野?
- ありがとうございます。これでP.73~P.77の内容が理解できたように思います! -- kero?
- P.70のラプラシアンの式で理解できない箇所があります。 ($\vec e_{r}$ d/dr)・($\vec e_{r}$ d/dr)の計算結果ですがd^2/dr^2でなく"0"ではないでしょうか? なぜなら左括弧内のd/drが右括弧内の$\vec e_{r}$を微分すると”0”になると考えるからです。 -- kero?
- ここで計算しているのはラプラシアンという微分演算子で、その演算子の後ろになにか微分されるもの(f(r,θ,φ)のような関数)があります。よって、(d/dr)は後ろにあるf(r,θ,φ)も微分します。そもそも、後ろの方の(d/dr)の更に後ろに何もないのだったら、答えはそこで0になってしまいます。 -- 前野?
- 確かにそのとおりです。 これで"よくわかる電磁気学"の演習問題2-5を理解することができました!! ところで前野先生は物理数学の本を出版される予定はないのでしょうか。 -- kero?
P79 12行目から13行目 部分積分 †
shoho? (2014-01-27 (月) 22:41:49)
初歩的な質問ですみません。
部分積分の左辺から右辺への変形で、部分積分の公式の、最初の項、∫に入っていない項はどうなるのでしょうか。消える理由を教えてください。
- 物理ではよく使う仮定ですが、fのような関数は「無限遠では0になっている」と考えます。この積分は-∞から∞までの積分なので、∫に入ってない項は±∞での値を出すことになるので、0です(この仮定が成り立たない場合はお釣りが残ることになります)。 -- 前野?
- ありがとうございます。今までにあったいくつもの疑問が解けました。先生の御本で勉強していきますので、またよろしくお願いします。 -- shoho?
P38右下の式(4刷) †
grabo? (2014-01-19 (日) 08:21:29)
$\mathrm{det}
\left(
\begin{array}{cc}
a &b \\
c &d
\end{array}
\right)$
に、$bc$を足すと$ad$になった。ではないでしょうか.
- すいません、そのとおりですね。次の版があれば直します。 -- 前野?
P73の上から3行目の式 †
k_shouda5336? (2013-07-15 (月) 06:48:06)
非常にいい本です。P73の上から3行目の式sinΔθの次はeθベクトルではないのでしょうか
- ありがとうございます。確かにp73のその式の最後は$\vec{\mathbf e}_\theta$(旧)です。 -- 前野?
P25 (第1刷) †
s2? (2012-12-25 (火) 10:15:56)
いまごろ第1刷の方を読んでおります。
P25の4行目の「傾きが${\beta - \alpha\over 2}$」というところと8行目の式の左辺を「$\sin \beta - \sin \alpha$」とされているところが理解できておりません。ヒントを頂けませんか?
- ${\beta-\alpha\over2}$になるのを理解するには、∠ABEが${\alpha+\beta\over2}$であることがわかる必要があります。それは(文章にもあるように)三角形ABEが二等辺三角形で、かつ頂角が$\pi-(\alpha+\beta)$だということ(ということは残り2つの角度は足して$\alpha+\beta$だということ)からわかります。 -- 前野?
- すいません、$\sin\beta-\sin\alpha$は$\sin\alpha-\sin\beta$の誤りですね。図のGEのところです。三角形AEGを考えると、これが$2\cos{\alpha+\beta\over2}\sin{\alpha-\beta\over2}$だと出てくるとおもいます。 -- 前野?
p105の誤植 †
しんどう? (2011-06-06 (月) 10:14:42)
ぱらぱらめくっていて見つけたので,とりあえず報告を.
第2刷のp105の一行目に,「疑問8で書いた仮想仕事の原理から」とありますが,仮想仕事の話は疑問9ですね.
- ありゃりゃ。LaTeXで原稿書いているのに、なぜにそんな間違いが紛れ込むのか…。次があったらなおしてもらいます… -- 前野?
仮想仕事の原理 †
機械学部? (2011-04-23 (土) 02:01:06)
仮想仕事の原理を御テキストでも扱っていらっしゃいますが、
ぜひとも『よくわかる「解析力学」』なるものを作っていただければ、
望外の喜びです。
先生のシリーズは、とっても分かりやすく、初心者に手厚いにもかかわらず、
十分な質のある内容と範囲の広さや量を抑えていらっしゃるので、
いつもお世話になっています。
- ありがとうございます。「よくわかる解析力学」は予定してないことはないのですが、まだまだ先のことになりそうです。 -- 前野?
- 先生にお返事いただけて、とても嬉しいです。 出版が遅くなると、その頃には -- 機械学部?
- その頃には、院生になってしまうかもしれませんが、それでも楽しみに待たせていただきます。 -- 機械学部?
p171 台詞 †
h2hisashiro? (2010-12-08 (水) 18:03:51)
第2刷では修正されたとありますが、まだ電場が D と H になっています。
- あれぇ??? 第3刷があれば必ず修正します(;_;)。 -- 前野?
p139 図の説明 †
ukatu? (2010-11-07 (日) 23:20:35)
楽しく、読ませていただいています。
p139の図の説明で、温度が下がらないと圧力も下がらないとありますが、等温変化の場合、pV=一定なので、図の場合だと体積が増えるので、圧力が下がると思います。断熱変化と比べてという事でしょうか?
- ああ、もちろん「断熱変化と比較して」とつけるべきところをうっかりしていますね。捕捉しておいてください。 -- 前野?
p77 †
ky生 11-7-10? (2010-11-07 (日) 01:04:12)
書店で衝動買い、楽しんで拝読中です。ネットでのサポート、ありがとうございます。ぜひとも続けてください。ところで質問です。
p77,下から4行目:偏微分の式で、単位ベクトルでの微分がよく理解できないのです。突然でてきてとまどっているのですが?
- 誤植です、すみません。単位ベクトルで微分するなんてできるわけないですね。これは「e_rで微分する」のではなく、「e_rをφで微分する」と書いたつもりでした。
 および、
および、 のように訂正してください -- 前野?
のように訂正してください -- 前野?
p79 †
MZT? (2010-08-09 (月) 11:06:12)
大変楽しく拝読させていただきました。そして勉強になりました。
p79ページの12行目の変分法ラプラシアンの展開式ですが、yの偏微分のところが偏微分の∂だけになっています。
あと私の勘違いかもしれませんが、6・7行目の内積は-がつくのでしょうか?マイナスが付くとすると、ピタゴラスの定理より出てくるsinΘ^2+cosΘ^2=1が成立せず、式の結果が出てこないのですが誤植でしょうか?
- ありがとうございますm(__)m。yは分母からちょっと下の方に脱走してますね。なぜ?? ところで6・7行目の内積ってのがどれのことだか、よくわかりません。p79とは別のページですか? -- 前野昌弘?
- すみません、p76です。>6・7行目の内積式。 -- MZT?
- ああ、ほんとだ。確認しました。6行目と7行目の第1項のマイナスは不要ですね。重ね重ねありがとうございましたm(__)m。 -- 前野昌弘?
P15 †
かし? (2010-07-22 (木) 21:38:36)
昨日買って、読み始めました。
ところで、p15に、スカラーは向きを表す
って書いてありますよ。
他にも誤植等あれば、ここで報告していただけると幸いです。
よろしくお願いしますね。
- ああ、すいません。「スカラーは大きさを表す」ですね。なんでこんな間違いを(;_;)。誤植については、サポートページの方で報告してますのでよろしく。 -- 前野昌弘?
P33の図のマイナス符号 †
なべ? (2010-06-28 (月) 22:14:52)
P33の図の中で、何故Δにマイナス符号が付くのか理解できませんでした。単純な質問ですみません。
- あの「Δなんとか」はみんな「長さ」を表現していると思ってください。だから当然、全部正の量です。図にある矢印のうち一番手前にある(∂x/∂y)を表現している矢印を見ると、矢印の根元から先へと行く時に、x座標が増えy座標が減ります。減ることを(Δyを正の量として)「−Δy変化した」と表現しているわけです。これでおわかりでしょうか? -- 前野昌弘?
- 考えてみれば、普通は「Δなんとか」は「なんとかの変化」を意味するから、あそこに「ここのΔx,Δy,Δzは全て正の量とする」と注釈つけておくべきでしたね。 -- 前野昌弘?
- すみません、再度お教えください。Δx=x2-x1, Δy=y2-y1として、∂x/∂y=lim(x2-x1)/(y2-y1)=Δx/Δy と考えてしまうのですが、Δyのマイナスの考え方をもう少し教えてください。 -- なべ?
- この場合ΔxとΔyは正になるように定義、なのでΔx=|x2-x1|、Δy=|y2-y1|です。P33の図で言うと、(x1,y1)=(0,Δy)で、(x2,y2)=(Δx,0)ですね。よって∂x/∂y=(Δx)/(-Δy)となるわけです。 -- 前野昌弘?
- 少し上にも書きましたが、ΔxとΔyは図に書き込んである部分の「長さ」で定義してます。注意を書いておかなかったのは私のミスですm(__)m。 -- 前野昌弘?
- なんとなく、わかってきました。今回の場合、(x,y)はz=一定の平面にある点ではなく、y軸上あるいはx軸上にある点と考えればよかったのですね。その辺でつまずいていたようです。丁寧にコメントいただきありがとうございました。物理の本を読むのは学生の時以来10年ぶりですが、むしろ年を経てからの方が物事の意味をじっくり考えるのが好きになりました。目次を見ると後半の方がより面白そうなので、次へ次へとどんどん読み進んで行きたいと思います。 -- なべ?
47ページの下から3行目 †
オリセー? (2010-06-27 (日) 21:37:50)
はじめまして。本日この本を手に取り読み始めたものです。
間違いじゃないかと思い書き込みしてます。
47ページの下から3行目の偏微分の定義式ですが、左辺最後のΔZ積ではなく分母側の間違いじゃないでしょうか。
- オリセー様、御指摘の通りですm(__)m。 -- 前野昌弘?
発売日です。 †
前野昌弘? (2010-06-05 (土) 13:50:12)
お買い上げ頂いた方、感想など書き込んで下されば幸いです。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)